Бурение грунтовых зондов, установка энергетических колодцев

Изложенные ниже данные приведены по результатам работы [50]. Жидкость циркулировала снизу вверх с постоянным расходом в течение 60—180 с, для того чтобы средний диаметр отверстия во льду составлял не более 0,043 м с целью предупреждения существенного различия карти­ны течения в стеклянных трубах, а также на участке теплообмена.

В качестве циркулирующих агентов использовались ньютоновские и неньютоновские жидкости, характеристики которых представлены в табл. 3.1. Значения вязкости рг и толщина пограничного слоя 6 в предпо­ложении устойчивости ламинарного потока приведены в табл. 3.2. Показа­тели п и k получены обработкой результатов измерений на вискозиметре «Фан», а теплопереносные свойства — на установке, использованной нами ранее [48]. Полные реологические кривые использованных в эксперимен­те жидкостей приведены в разделе 1.1.

Составим условие теплового баланса

TOC o "1-5" h z = nDaTh. (3.1)

Согласно работе [45]

= 1,76Я[(<?/(аА)]1/3. (3.2)

Подставляя выражение (3.2) в (3.1), получаем

V — KQ, (3.3)

где V = n(D2-D$)h/(4Tty, Q = [(<?»/(аЛ)]1/3; К= l,76nXh/(WQ2q).

Для учета различия вязкости основного потока и пограничного слоя воды, образующегося при таянии льда, используем поправку Зидера — Тейта

* = W|x.)0U. (3-4)

Пограничный слой воды — ньютоновская жидкость. Поэтому эффек­

тивную ньютоновскую вязкость основного потока представим в дифферен­циальной форме

Иг = dt/dy. (3.5)

Скорость сдвига

(36)

г 4 п D

Таблица 3.1 Циркулирующая жидкость Температура Г, °С Степень неньютоновского поведения п Вода 20 1 Водные растворы: глицерина 28 1 (Q<20) глицерина 28 1 (Q>20) Na-бентонита 20 0,3 Na-КМЦ 20 0,75

Плотность е, кг/м3

Теплоемкость с, Дж/(кг-°С)

998,2 1130 1180 1040 1016

4186 2720 2510 4100 4180

Показатель консистенции k, Па-с

0,001

0,007

0,018

1,8

0,32

Тепло­проводность к, Вт/(м-°С)

0,6

0,41

0,37

0,62

0,6

Значения толщины пограничного слоя воды б, 10 6 м (знаменатель), и вязкости жидкости Ц2, Ю_3 Па-с (числитель), при разных Q

Жидкость	Q
7,5	10	12,5	15	17,5	20	22,5	25
Вода Водные	1/260	1/150	1/84	1/66	1/60	1/50	1/38	1/26
растворы: глицерина 7/374 7/210 Na-бенто — 270/566 135/309	7/125 96/183	7/93 66/120	7/69 43/84	18/60 32/65	18/48 24/51	18/39 20/41
нита
Na-КМЦ 196/530 164/294 139/185 122/129	110/98	98/73	90/56	81/49

При обработке экспериментальных данных необходима гидродинами­ческая поправка на успокоительный участок — стеклянную трубу [45]

(3.7)

е = 0,6(1+2,5ф)/фо-мз,

где ф = np.2//(4e2Qi).

С учетом соотношений (3.4) и (3.7) выражение (3.3) принимает вид

(3.8)

V/K= Q/фе.

С учетом малой толщины пограничного слоя воды из выражений (3.1) и (3.2) получим

(3.9)

6(A) = l,76nCQTDilpe,/(4Wii2qQ2).

Экспериментальные данные на рис. 3.2 можно представить выраже­ниями:

(3.10)

вязкостной режим течения

V/K=Q,

(3.11)

что совпадает с теоретической зависимостью (3.8), так как фе = 1; вязкостно-гравитационный режим течения

V/ К = 0.57Q+9.

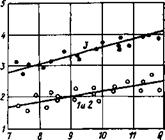
■ Рис. 3.2. Удельная скорость каверно- образования при циркуляции воды.

1 — расчет по формуле (3.3); 2 и 3 — экс­перимент; 2 — вязкостной режим течения воды, 3 — вязкостно-гравитационный.

Приравнивая выражения (3.10) и (3.11) [предполагаем справедли­вость выражения (3.11) в диапазоне 12<1Q<;21], получаем Q = 21 и Qi — = 0,32-10_3 м3/с. При большем расходе воды исчезает влияние гравитации на теплоотдачу: вязкостно-гравитационный режим течения переходит в вязкостной и наоборот. Расчет по формуле (3.9) при Q = 21 дает тол­щину устойчивого’к гравитации пограничного слоя воды 6 = 0,034-10~3 м.

Обозначения в формулах (3.1) — (3.11) имеют следующий смысл: Do и р — начальный диаметр рабочего элемента из льда или мерзлой породы и средний диаметр после теплообмена; Л — высота рабочего элемента; WQ2 »Q — массовое содержание льда в единице объема породы и скрытая теплота плавления льда; а — коэффициент теплоотдачи; Tut — темпера­тура и время циркуляции жидкости; к — теплопроводность жидкости; Qi и а — расход и температуропроводность жидкости; |Ai и |л2 — вязкость пограничного слоя воды и циркулирующей жидкости; Лил — показатели консистенции и неньютоновского поведения жидкости; I — длина стеклян­ной трубы; р — плотность циркулирующей жидкости; с — массовая тепло­емкость жидкости; б — толщина пограничного слоя воды; v — средняя скорость течения Жидкости.

В случае вертикального расположения трубы и противоположного направления свободной и вынужденной конвекции у стенки [45], подавле­ние или возникновение гравитации происходит при фиксированном зна­чении отношения

Аг яд04Ао

(3.12)

Rei 4mQi

где Аг = pgD3Ao/p? — число Архимеда; Re = vDq/ii — число Рейнольд­са; g — ускорение свободного падения; D — средний диаметр отверстия в рабочем элементе после теплообмена; Др — разница плотностей основ­ного потока и пристенного слоя воды; pi — вязкость пристенного слоя воды; Qi — расход циркулирующей жидкости.

Подставляя в выражение (3.12) g = 9,81 м/с2, Др = 1,7 кг/м3, |i| = = 1,3-10-3 Па-с (здесь и в дальнейшем вязкость пристенного слоя воды принимаем при температуре 10°С, средней между температурой основно­го потока и пристенного слоя), Qi = 0,32-10-3 м3/с и D = 0,047 м (макси­мальный в эксперименте диаметр отверстия в рабочем элементе), получа­ем Ar/Rei = 154. Если аналогично работе [45] определить отношение Gr/Rei (где Gr — число Грасгофа), то получим значение 108, что более чем в 2 раза ниже результатов работы [45]. Такое отличие можно объяс­нить специфичными условиями теплообмена, которые существенно отли­чались от условий опытов в работе [45], где отсутствовало плавление стенок трубы с образованием новой фазы.

Из данных рис. 3.2 следует, что влияние гравитации может быть весьма существенным. Так, например, для Q’= 7 теплоотдача при вяз­костно-гравитационном режиме в 2 раза выше, чем в случае вязкостного режима. С повышением расхода воды влияние гравитации постепенно уменьшается. Полагая в выражении (3.11) Q = 0, получаем V -108 = 2,4, т. е. кавернообразование при свободно-конвективном движении соответст­вует развитому ламинарному режиму (3.10).

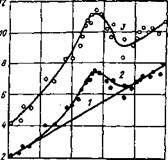
W1 и3/(с °су Рис — 3-3. Удельная скорость каверно-

в 12 16 20 24 9

’ образования во льду при циркуляции

водного раствора Na-бентонита.

/ — расчет по формуле (3.3); 2—экс­перимент, деленный на численное значение поправок (3.4) и (3.7); 3 — эксперимент.

На рис. 3.3 представлены данные, полученные при циркуляции вод­ного раствора Na-бентонита. Когда Q = 12,7, начинается отклонение экс­перимента от линейной зависимости. Специфической особенностью экс­перимента является увеличение внутреннего диаметра рабочего элемента вследствие таяния льда, т. е. при постоянном расходе жидкости число Rei обратно пропорционально диаметру. Принимая D = 0,036 м, pi = = 1,3-10-3 Па-с и Q = 12,7, получаем Rei = 2013. Таким образом, откло­нение эксперимента от линейной зависимости происходит в момент нару­шения ламинарного режима течения пограничного слоя воды, когда теплоотдача резко возрастает с увеличением числа Рейнольдса.

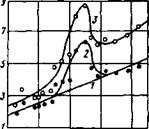
На рис. 3.4 представлены данные, полученные для водного раствора глицерина. Свойства жидкости приведены в табл. 3.1. Качественно экспе­риментальная зависимость соответствует данным рис. 3.3, однако имеются некоторые количественные отличия: отклонение эксперимента от линейной зависимости начинается при большем значении Rei = 3729 и несколько выше максимальное значение V. Остановимся на этом вопросе.

Дело в том, что в условиях кольцевого двухфазного течения при лами­нарном режиме основного потока турбулизация пристенного слоя, видимо, возможна при определенном условии: двухфазный поток жидкости должен быть гравитационно неустойчив. Действительно, турбулизация пристенно­го слоя приводит к росту гидравлических сопротивлений, поэтому ско­рость в ядре потока должна уменьшиться. Нарушение устойчивости в ядре

Ю 14 18 22 24 Q

У, Ю $м,/(с Х) Рис. 3.4. Удельная ско­

рость кавернообразования во льду при циркуляции водного раствора глицери­на.

1 — расчет по формуле (3.3); 2 — эксперимент, де­ленный на численное значе­ние поправок (3.4) и (3.7);

3 — эксперимент.

потока происходит при определенных числах Аг, возрастающих с увели­чением Re2. Расчет с использованием значений из табл. 3.1 и 3.2 и D = = 0,047 м на момент отклонения эксперимента от линейной зависимости дает для водных растворов Na-бентонита и глицерина следующие резуль­таты: Re2 = 22, Аг = 4664, Ar/Re2 = 212 и Re2 = 438, Аг =

= 3,06-106, Ar/Re2 = 6979. Из сопоставления полученных результатов представляется естественным предположить, что затягивание перехода ламинарной формы течения пограничного слоя воды в турбулентную (см. рис. 3.4) объясняется высоким значением числа Архимеда, т. е. форми­рованием более выпуклого и устойчивого профиля скорости в пристенном слое. Резкий переход через критическое число Рейнольдса, видимо, связан с тем, что появление турбулентных пульсаций в затянувшемся ламинарном потоке ускоряет рост теплоотдачи [45]. Более высокое мак­симальное значение V на рис. 3.4 можно объяснить тем, что при переход­ном режиме течения пограничного слоя воды определенное влияние на теплоотдачу оказывает свободная конвекция [45].

Максимум на рис. 3.3 и 3.4 может быть объяснен конкуренцией двух факторов. С одной стороны, при возрастании Q повышается градиент ско­рости на стенке рабочего элемента, происходит рост пика пульсаций и коэффициента перемежаемости [45]. Однако повышение Q уменьшает толщину пристенной пленки воды, что следует из выражения (3.9). Проис­ходит своеобразный «отсос» пограничнчго слоя и постепенное подавление турбулентности от входа к выходу из участка теплообмена, поскольку тол­щина пограничного слоя (3.9) от входа к выходу увеличивается. Первый из факторов стимулирует, а второй подавляет теплообмен. При значени­ях Q левее максимума доминирует первый фактор, а правее второй. Следу­ет отметить, что максимум V соответствует одному значению Q = 19 и Rei = 6500.

При Q = 23 экспериментальная зависимость на рис. 3.3 и 3.4 принима­ет прямолинейный характер, т. е. режим течения пограничного слоя воды на всей длине участка теплообмена становится ламинарным, хотя число Rei составляет около 104. Это число соответствует развитой турбулент­ности, при которой практически исчезает влияние свободной конвекции на теплоотдачу [45], т. е. двухфазный поток вновь приобретает гравита­ционную устойчивость. Толщина пограничного слоя воды, при которой происходит подавление турбулентных пульсаций составляет около 5- КГ5 м (см. табл. 3.2). Этот результат удовлетворительно соответствует полученному выше значению 3,4 • 10-5 м, когда циркулирующей жид­костью была вода. Такое совпадение можно объяснить тем, что в том и другом случае потеря пограничным слоем воды ламинарной формы тече­ния связана с гравитацией.

На рис. 3.5 приведены данные, полученные при циркуляции водного раствора Na-КМЦ. Особенность полученных результатов в сравнении с приведенными на рис. 3.3 и 3.4 состоит в том, что экспериментальные данные не отклоняются от линейной зависимости. Расчет с использовани­ем данных табл. 3.1 и 3.2 и D — 0,047 м при Q — 12,7 (аналогично раство­ру Na-бентонита) дает Re = 14, Аг = 812 и Ar/Re2 = 58. Таким образом, отсутствие экстремальных значений на рис. 3.5 видимо связано с малым

отношением Ar/Re2, т. е. поток водного раствора Na-КМЦ гравита­ционно устойчив.

Визуальный осмотр показывает, что при ламинарном режиме пристен­ного слоя воды (см. рис. 3.2 и 3.3) диаметр отверстия закономерно умень­шается от входа к выходу из участка теплообмена. Для вязкостно­гравитационного режима (рис. 3.2), а также в области аномалии (см. рис. 3.3 и 3.4) характерна цилиндрическая форма отверстия, т. е. коэффи­циент теплоотдачи практически не изменяется по длине рабочего элемен­та. Совпадение экспериментальных данных с расчетом по формуле (3.8) показывает, что соотношение (3.5) в отличие от обычно используемого представления [64] физически более оправданно.

Следует обсудить еще одну особенность. Дело в том, что эксперимен­ты с однофазным потоком [45] при совпадении направления вынужден­ной и свободной конвекции в пристенном слое показывают существенное влияние свободной конвекции на теплоотдачу при числах Рейнольдса ни­же критических. Двухфазный поток водных растворов Na-бентонита и гли­церина при ламинарном течении потенциально неустойчив. Однако дей­ствие гравитации не проявляется, что можно объяснить стабилизирующим действием основного потока циркулирующей жидкости. Только при появ­лении поперечных пульсаций в пограничном слое воды двухфазный по­ток становится гравитационно неустойчив.

Интересно отметить, что критические числа Рейнольдса, при которых начинается отклонение эксперимента на рис. 3.3 и 3.4 от линейной зави­симости, соответствуют характерным — экстремальным точкам графика Никурадзе, закона сопротивления для течения в гладкой трубе: при Rei = = 2013 заканчивается ламинарный режим течения пограничного слоя воды, а при Rei = 3729 начинается развитие устойчивой турбулентности.

Комментарии запрещены.