Бурение грунтовых зондов, установка энергетических колодцев

Изучение теплообмена в вертикальных кольцевых трубах с наруж­ной плавящейся стенкой и теплоизолированной внутренней представляет

большой научный и практический интерес. Примером является плавление мерзлых пород или льдов при бурении скважин.

)Кидкость циркулировала снизу вверх с постоянным расходом по трубе концентричного кольцевого сечения и последовательно проходила нижний успокоительный участок длиной 1,2 м, участок теплообмена дли­ной 0,25 м и верхний успокоительный участок длиной 1,2 м. Диаметры кольца на успокоительных участках составляли 0,016 и 0,038 м. Участок теплообмена представлен льдом цилиндрической формы с диаметрами

0,036 и 0,1 м при температуре —1-i————— 2°С. В процессе плавления льда

диаметр возрастал и в среднем составлял 0,041 м. Таким образом, на участке теплообмена имеем кольцевое двухфазное течение: пограничный слой воды, образующейся при таянии льда и основной поток циркулиру­ющей жидкости.

Влияние вязкости фаз также учитываем поправкой Зидера—Тейта

‘l> = W|ii)0,14- (3.13)

Вода в пограничном слое является ньютоновской жидкостью с вязкостью in. Поэтому по аналогии с круглой трубой введем понятие об эффек­

тивной ньютоновской вязкости основного потока иг. Воспользуемся сте­пенной реологической моделью

т = *у*. (3.14)

Из подстановки этой зависимости в дифференциальную форму закона Ньютона (i2 = dx/dy получим

lb _ nlkf-i, (3.15)

где у = 12tT(2n+l)/[3n(D—rf)]; Dud — средний диаметр участка тепло­обмена после циркуляции жидкости и наружный диаметр внутренней тру­бы или, другими словами, (D—d) — эквивалентный диаметр кольцевой трубы.

Поправка на успокоительный участок не требуется, так как его длина достаточна для формирования профиля скорости.

На ЭВМ ЕС-1022 для ламинарного потока однофазной конвективно устойчивой жидкости в кольцевой трубе с теплоизолированной внутренней стенкой выполнена численная обработка решения [45] в безразмерном виде

*Н._,,42(р4-)»’, (3.16)

где (Ре Л/0 = 102Ч-104; погрешность Nu<0,017.

Выражение (3.16) совпадает с экспериментом при малой толщине пограничного слоя воды, когда течение можно представить как поток однофазной конвективно устойчивой жидкости. Отсюда следует, что диф­ференциальная форма (3.15) физически более оправдана. Выражение (3.16) и соответствующий эксперимент назовем базовыми.

11 (Peh/l),/3

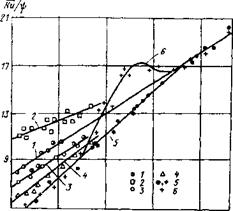
Рис, 3.6. Удельная ско­рость кавернообразования во льду при течении жид­кости через кольцевую трубу.

1—3 — вода при темпера­туре 5; 20 и 30 °С; 4 — вод­ный раствор Na-КМЦ с вяз­костью 0,008 Па-с; 5— вод­ные растворы Na-бентоннта и Na-КМЦ; 6 — водный раст­вор Na-бентонита.

5

7

9

Кроме базовой зависимости / на рис. 3.6 имеется три типа данных, ко­торые различаются физической природой: гравитационная турбулиза­ция 2, нарастание толщины пограничного слоя 3—5 и пульсационная турбулизация 6.

1. Гравитационная турбулизация. При циркуляции воды с температу­рой 30°С получена зависимость

(3.17)

Плотность пограничного слоя воды выше плотности основного потока, т. е. направления свободной и вынужденной конвекции у плавящейся стенки будет противоположными, а режим течения воды на участке тепло­обмена вязкостно-гравитационным. Это приводит к усилению теплоотда­чи относительно базовой зависимости 1 в связи с гравитационной турбу — лизацией. По аналогии с круглой трубой (см. раздел 3.1) допустим, что появление гравитационной турбулизации наступает при фиксированном значении отношения

(3.18)

Ar/Re2 = ng(D—d)D+ОДс/(4ц2 Q<),

где Ar = Qg(D—d)3AQ/n$ — число Архимеда; Re2 = v(D—d)Q/n2 — число Рейнольдса. .

Остальные обозначения соответствуют формуле (3.12). Другими сло­вами, различие выражений (3.12) и (3.18) состоит в замене диаметра круглой трубы на эквивалентный диаметр кольцевой трубы.

Из формул (3.16) и (3.17) следует, что гравитационная турбулизация появляется при (Рей//)1/3= 10,8. Определим отношение (3.18) при сле­дующих данных: (Рей//),/3 = 10,8; температура циркулирующей воды 30°С и плавящейся стенки 0°С, т. е. Aq = 4,2кг/м3 и р2 = 1,15* 10~3 Па*с; D = 0,046 м; d = 0,016 м; Qi = 0,29 • 10-3 м3/с. Подстановка в выражение (3.18) дает Ar/Re2 = 162. Интересно отметить, что аналогичный экспе­
римент в круглой трубе (см. раздел 3.1) дает такое же значение Ar/Re2. другими словами, при расчете критерия гравитационной турбулизации в трубе кольцевого поперечного сечения характерным размером является эквивалентный диаметр D—d. Важным является то, что аналогичная картина справедлива для пульсационной турбулентности: критическое число Рейнольдса имеет одно значение для труб круглого и кольцевого поперечного сечения, когда в качестве характерного размера также прини­мается диаметр круглой трубы и эквивалентный диаметр D — d трубы коль­цевого сечения [45]. Такая аналогия имеет, видимо, глубокий смысл, поскольку в обоих случаях наблюдается один физический процесс — нару­шение ламинарной формы течения и возникновение турбулентности. Различна только природа турбулизации: гравитационная или пульсацион — ная.

2. Нарастание толщины пограничного слоя. Особенность эксперимен­та 3—5 выражается в снижении теплоотдачи относительно базовой за­висимости 1. Физически этот процесс можно пояснить следующим обра­зом. Режим течения основного потока жидкости и пограничного слоя воды является ламинарным, т. е. их перемешивания не происходит. Поэтому толщина пограничного слоя воды вследствие таяния льда возрастает от входа к выходу из участка теплообмена. Из уравнения теплового балан­са следует, чем ниже значение (РеА//)|/3, тем выше толщина погранич­ного слоя б, поскольку согласно формуле (3.9) 6~фГ2/3- С другой сторо­ны, специфика теплообмена такова, что поправка (3.13) справедлива в непосредственной близости от поверхности теплообмена. Поэтому, когда пограничный слой воды превышает определенную толщину, поправка

(3.13) начинает действовать в пределах этого слоя, где ф-»-1. По мере снижения (РеЛ//)1/’3 длина пристенного слоя воды, в пределах которого ф-»-1, увеличивается от выхода к входу, а при (РеЛ//)1/3^5 становится равной длине участка теплообмена. Этот результат также справедлив для потока однофазной жидкости [45].

3. Пульсационная турбулизации. При значении (РеА//) 1/3=7,7 экс­перимент с раствором Na-бентонита отклоняется от прямой 5 и, проходя че­рез максимум, выходит на базовую зависимость 1. Определим отношение Аг/Яег в момент выхода 6 на базовую зависимость 1 (вторая критиче­ская точка) при следующих данных: £> = 0,048 м, d = 0,016 м, ег = = 1040 кг/м3 и pi = 1000 кг/м3, т. е. До = 40 кг/м3, рг = 0,013 Па • с; Qi = = 0,33* 10_3 м3/с. Из выражения (3.18) получим Ar/Re2 = 147.

Допустим, что и в первой критической точке [при (РеА//)1/3 = 7,7] чис­ло Ar/Re2 — 147. Используя метод последовательных приближений, из условия (РеА//)1/3=7,7 и Ar/Re2=147 получаем £>=0,039 м. Дру­гими словами, при среднем диаметре цилиндра из льда 0,039 м происхо­дит отклонение б от зависимости 5.

Определим режим течения пограничного слоя воды в первой критиче­ской точке при следующих данных: (РеА//)1/3 = 7,7; Qi =0,118-10~3 м3/с; 0i = Ю3 кг/м3; d = 0,016 м; температура раствора бентонита 20°С и пла­вящейся стенки 0°С, т. е. pi = 1,3-10-3 Па-с. Получим Rei =2100.

49

Таким образом, отклонение 6 от прямой 5 происходит при следующем условии: Ar/Re2= 147 и Rei =2100. Если одно из чисел меньше указан-

4 Заказ 1935
ных значений, то зависимость 5 будет иметь линейный характер. Это подтверждается в экспериментах с водным раствором Na-КГМЦ, для ко­торого число Рейнольдса пограничного слоя воды в первой кри­тической точке равно 2100, но Ar/Re2 = 59. Другими словами, турбулиза­ция пристенной фазы — пограничного слоя воды возможна в случае гра­витационной неустойчивости двухфазного потока. Физически, аналогично эксперименту с круглой трубой, это также можно объяснить резким воз­растанием гидравлических сопротивлений при турбулизации пограничного слоя воды, поэтому скорость в ядре потока должна уменьшиться. Условием такой деформации профиля скорости является неустойчивость кольцевого двухфазного потока.

Следует обсудить одну особенность. Эксперименты с однофазным по­током [50] при совпадении направлений свободной и вынужденной кон­векции в пристенном слое показывают существенное влияние грави­тации на теплоотдачу. При ламинарном течении водного раствора Na-бен­тонита и пограничного слоя воды, т. е. при (Рей//)1/3<7,7, двухфазный поток потенциально неустойчив, однако действие гравитации не проявля­ется. Гравитационная неустойчивость зарождается, когда Rei = 2100, т. е. при появлении поперечных пульсаций. Другими словами, в кольцевом двухфазном течении оба рассмотренных фактора также взаимосвязаны.

По аналогии с экспериментом раздела 3.1 экстремальный характер кривой 6 можно объяснить конкуренцией двух факторов. С одной стороны, при возрастании (РеА//)1/3 повышается градиент скорости на плавящейся стенке из льда, происходит рост пика пульсаций и коэффициента пере­межаемости. С другой стороны, из уравнения теплового баланса следует, что при возрастании (РеА//)1/3 снижается толщина пограничного слоя воды [см. выражение (3.9)], т. е. происходит своеобразный «отсос» по­граничного слоя и постепенное подавление турбулентности от входа к вы­ходу из участка теплообмена.

Визуальный осмотр отверстия во льду показывает, что в области ано­малии для развитого процесса пульсационной турбулентности характерна цилиндрическая форма отверстия. Такая же картина наблюдается при гравитационной турбулентности (кривая 2 на рис. 3.6). В остальных слу­чаях диаметр отверстия закономерно уменьшается от входа к выходу, что соответствует характеру теплообмена при вязкостном режиме течения. Первый результат (цилиндрическая форма отверстия) подтверждает тур- булизацию и перемешивание пограничного слоя воды и основного потока, так как тепловое сопротивление по длине участка теплообмена постоянно. При ламинарном течении перемешивания фаз не происходит, поэтому рост толщины пограничного слоя воды от входа к выходу из участка тепло­обмена приводит к росту теплового сопротивления и параллельному сни­жению диаметра отверстия во льду.

Интересно отметить следующие результаты: 1) критические значения Ar/Re2 двухфазного потока практически одинаковы при плотности погра­ничного слоя воды выше плотности основного потока и наоборот; для однофазного потока [45] такая закономерность не выполняется; 2) все экспериментальные кривые на рис. 3.6 пересекаются в одной области, где толщина пограничного слоя воды становится достаточно малой (0,06—

О ОЙ мм), а затем вырождаются в прямую 1. Видимо начиная с этих значе­ний исчезают рассмотренные выше особенности, т. е. эксперимент соот­ветствует классическому теплообмену при вязкостном течении однофазной несжимаемой и конвективно устойчивой жидкости.

Полученные в разделах 3.1 и 3.2 результаты использованы при обосно­вании технологии бурения мерзлых пород в гл. 6.

Комментарии запрещены.