РЕОЛОГИЧЕСКИЕ МОДЕЛИ ПРОМЫВОЧНЫХ ЖИДКОСТЕЙ
РЕОЛОГИЧЕСКИЕ МОДЕЛИ ПРОМЫВОЧНЫХ ЖИДКОСТЕЙ
Одной из основных функций промывочной жидкости является обеспечение устойчивости ствола скважины — предупреждение кавернообра — зования. Исследования показывают, что предупредить или резко ограничить кавернообразование можно путем поддержания определенных реологических показателей. Промывочные жидкости являются сложными системами, и реологического закона для них обычно не существует. Поэтому для характеристики потока используют приближенные закономерности, называемые моделями. Прежде чем перейти к реологическим моделям промывочных или цементных растворов, остановимся на фундаментальном законе, называемом законом трения Ньютона. Целесообразность этого обусловлена двумя основными причинами: 1) закон трения Ньютона — базовая часть реологических моделей; 2) жидкая фаза промывочных и цементных растворов обычно является ньютоновской жидкостью, вязкость которой оказывает существенное влияние на реологию растворов.
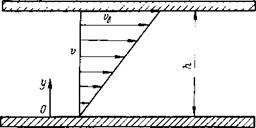
Рассмотрим течение ньютоновской жидкости между двумя параллельными пластинами (рис. 1.1). Нижняя пластина неподвижна, а верхняя движется в собственной плоскости с постоянной скоростью vB. Опыт показывает, что жидкость прилипает к обеим пластинкам. Поэтому, скорость жидкости около нижней пластины будет равна нулю, а возле верхней равна vB. Опыт также показывает, что распределение скоростей жидкости между пластинами является линейным:
v = vBy/h. (1.1)
Выражение (1.1) в буквенной форме представляет результаты опытов: при у=О (нижняя неподвижная пластинка) о=0, при y=h (верхняя подвижная пластина) v=vB.
Чтобы существовало течение, изображенное на рис. 1.1, между жидкостью и верхней пластиной должна иметь место сила трения. Опыт по-
|
|
Рис. 1.1. Распределение скоростей в ньютоновской жидкости между параллельными плоскими стенками при движении верхней стенки вправо.
называет, что эта сила (на единицу площади пластины — напряжение трения) пропорциональна скорости верхней пластины ив и обратно пропорциональна расстоянию между пластинами Л:
т = щ»в/й. (1.2)
Если в пространстве между пластинами выделить тонкий слой жидкости dh, то выражение (1.2) примет общую форму
т = pdv/dh = ру. (1.3)
Коэффициент пропорциональности р, зависит от природы жидкости. Он мал, например, для воздуха, воды или спирта, но велик для масел и глицерина. Таким образом, р есть физическая характеристика жидкости, называемая динамическим коэффициентом вязкости или просто вязкостью жидкости. Равенство (1.3) называют законом трения Ньютона. Он точно описывает картину течения простых жидкостей, называемых ньютоновскими. К ним относятся все газы, жидкости и растворы с небольшой молекулярной массой (вода, минеральные масла, водные растворы солей, спирты, глицерин, бензин, дизтопливо, беспарафинистые нефти и т. п.). К этому классу можно отнести ньютоновские жидкости с малым содержанием частиц твердой фазы, которые не оказывают друг на друга взаимного влияния. Более подробно на системах такого рода остановимся в дальнейшем.
|
|
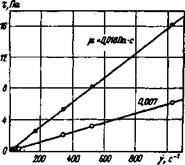
Экспериментальная зависимость т—у ньютоновской жидкости — водного раствора глицерина — приведена на рис. 1.2. Жидкости с такими свойствами использовались в опытах, описанных в гл. 3. График представляет собой прямую линию, выходящую из начала координат, и вязкость есть тангенс угла наклона прямой к оси ц = т/^. Физический смысл вязкости в качестве меры передачи количества движения от одного слоя к другому (см. рис. 1.1) в основном связан с особенностями поведения жидкостей при сдвиговых деформациях: вязкость — сила трения на единицу площади между слоями жидкости, отстоящими друг от друга на единичном расстоянии, при единичной разности скоростей между ними. Таким образом, для ньютоновских жидкостей при установившемся ламинарном
Рис. 1.2. Реологическая зависимость ньютоновской жидкости (водного раствора глицерина) с различной вязкостью при 28 °С.
течении характерно наличие одного напряжения трения, которое согласно закону (1.3) пропорционально градиенту скорости сдвига и обусловлено вязкостью.
В отечественной практике применительно к буровым и тампонажным растворам используют модель трения Шведова — Бингама
т = io—Tdv / dh = то+цу. (1.4)
Согласно выражению (1.4) для установившегося ламинарного потока буровых жидкостей характерно два вида напряжений трения: 1) вязкостное трение, пропорциональное градиенту скорости сдвига цу, т. е. соответствующее равенству (1.3); 2) динамическое напряжение сдвига, обусловленное трением твердых частиц, то. По этой причине промывочные или цементные растворы, удовлетворяющие зависимости (1.4), называют вязкопластичными или бингамовскими. При т0 = 0 модель (1.4) переходит в закон Ньютона (1.3), т. е. пластическая вязкость ц принимает смысл динамической или ньютоновской вязкости. Таким образом, модель (1.4) характеризуется двумя реологическими постоянными: пластической вязкостью и динамическим напряжением сдвига.
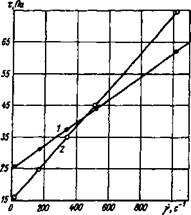
В качестве примера жидкостей, удовлетворяющих модели Шведова — Бингама (1.4), на рис. 1.3 приведены результаты реологических измерений раствора портландцемент — вода через 2 мин перемешивания и портландцемент — этиловый спирт. Объемная концентрация твердой фазы — портландцемента — принималась равной 0,39. Результаты измерений имеют прямолинейный характер, т. е. вязкость систем не зависит от скорости сдвига и равна т) = (т—то)/у. Прямолинейный характер зависимости т — у объясняется тем, что в течение малого периода перемешивания портландцемента и воды не успевают образоваться продукты реакции коллоидного размера, обладающие молекулярными силами сцепления. В системе цемент — спирт сцепление частиц твердой фазы отсутствует вообще. Из данных рис. 1.3 следует, что в растворах такого типа динамическое и статическое напряжения сдвига равны между собой: то=0. Анало-
|
|
Рис. 1.3. Реологическая зависимость неньютоновских жидкостей при 20 °С.
1—портландцемент—этиловый спирт (то=25 Па, i)=0,036 Па-с); 2 — портландцемент— вода (то=15 Па, »i= =0,06 Па-с).
г, Па
|
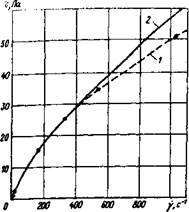
Рис. 1.4. Реологическая кривая водного раствора Na-КМЦ при 20 °С. 1 — эксперимент; 2 — расчет для л=0,75 и £=0,32. |
|
при 20 °С. 1 — эксперимент; 2 — расчет для л=0,3 и £=1,8. |
гичная картина будет иметь место для промывочных жидкостей с грубодисперсной твердой фазой.
Если в растворе имеется дисперсная фаза коллоидной фракции, то экспериментальная зависимость имеет непрямолинейный характер (рис. 1.4—1.6). Непрямолинейный характер кривой т —у объясняется тем, что при более высоких скоростях сдвига молекулярные связи между частицами коллоидной фракции разрушены в большей степени. Начиная с определенных значений скоростей сдвига эти связи разрушаются полностью и зависимость принимает прямолинейный характер. Продолжение прямолинейного участка реологической кривой до пересечения с осью ординат дает динамическое напряжение сдвига, а тангенс угла наклона к оси абцисс — пластическую вязкость. Таким образом, для растворов с непрямолинейной зависимостью т —у модель (1.4) справедлива в диапазоне скоростей сдвига соответствующих прямолинейному участку кривой.
Более широкий диапазон изменения скоростей сдвига можно охватить с использованием степенной модели Рейнера—Оствальда
|
(1.5) |
т = ky
где к ил — показатели консистенции и неньютоновского поведения промывочной жидкости.
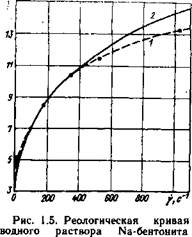
При л = 1 выражение (1.5) трансформируется в равенство (1.3), т. е. модель Рейнера — Оствальда переходит в закон Ньютона, а показатель консистенции принимает смысл динамической вязкости. Модель (1.5) может точно описать кривую течения (рис. 1.4) в широком диапазоне скоростей сдвига, но в большинстве случаев справедлива в определенном и подчас узком диапазоне изменения у- Примеры такого рода приведены на рис. 1.5 и 1.6. Исследованные здесь жидкости использовались в экспериментах, описанных в гл. 3.