Бурение грунтовых зондов, установка энергетических колодцев

Как видно из рассмотрения различных реологических моделей, для точного отнесения их к той или иной жидкости, прежде (всего надо уметь правильно определять величину градиента скорости. Однако, если для вязких жидкостей эта задача решается достаточ­но просто, то для неньютоновских систем ее решение весьма за­труднительно, так как существующие приборы (вискозиметры) не — дают возможности получить точную картину взаимосвязи между т и dujdy. Переход от координат расход — давление (Q—Р) к коор­динатам т—du]dy фактически исключен, так как, работая на капил­лярном вискозиметре, можно говорить лишь о величинах средней объемной скорости и касательного напряжения на стенке трубки, а не в любой точке живого сечения канала.

При использовании ротационных приборов приходится иметь дело с вращением массы испытуемой жидкости, что намного от­личается от условий движения этой же жидкости в капиллярных вискозиметрах, что опять-таки приводит к погрешностям.

Все отмеченное выше привело к поискам методик, которые учитывали бы все эти обстоятельства. В настоящее время из таких методик наибольшее внимание привлекает методика, предложен­ная Метцнером и Ридом, в основу которой положены исследова­ния Рабиновича, Муни, Ачвиса, Бочера и Пигфорда. В кратком изложении сущность всех этих исследований может быть пред­ставлена в следующем виде. —

/

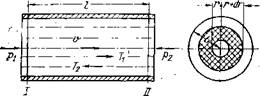
, Рис. 2. Схема движения потока на участке цилин­дрической трубы

п

Расход любой жидкости в круглой трубе радиуса R в самом общем виде может быть найден из выражения •

R R Q — J 2mudr = n ( ud (г*),

которое при условии, что жидкость на стенках прилипает, т. е. отсутствует скольжение и и(Р)=0, после интегрирования по ча­стям приводится к виду R . Q=n f гЧи, (11.17) о тде г — текущий радиус; и — текущая скорость. В случае движения в трубе стационарно-реологической жидко­сти, т. е. жидкости, свойства которой не зависят от времени и опи­сываются реологическим уравнением типа (II.2), для отыскания значения du можно воспользоваться условием равновесия некото­рого объема жидкости в трубе (рис. 2): . 2nrlr = nr2p, (11.18) юткуда легко получаются следующие соотношения:

21 / с г=/? 21 7 ‘ R Тогда выражение (II.2) с учетом (11.19) запишется в виде У = —= /(х) = /(тс-£-) и Ди= f(rc^-) dr. (11.20)

(II. 19)

(11.16)

ЕЕ.: 21 ’

/Р

т = —

т= х.

Подстановка (11.20) в (11.17) дает

Q = я J г2/ ^тс dr. (II.21>

Наконец, имея в виду, что на основании (11.19)

TOC o "1-5" h z т/? „ R

г ———- ; г2 = ■—— ; dr =—dt, .

. Те те ’

и подставляя эти значения в (11.21), находим:

и ^2^2 . п т р R3 X

‘ Q = n J ‘Т Ч )-£dr = n — J T2/(T)dT. (11.22)

о. V r R J тс тс • .

Подставляя в (11.22) конкретные значения для f(x) и интегри­руя, можно получить выражение расхода для различных реологи­ческих моделей. Так, принимая x=idu/dy и подставляя f(x)~ =du/dy=т/р, получаем известную формулу Гагена — Пуазейлж для расхода ньютоновской жидкости:

Q = -—• ? T3dr = ЛЮ., (11.23)

TOC o "1-5" h z Jo W

Подстановка %=rdu/dr+xo (тело Шведова — Бингама) приво­дит к выражению, которое в литературе известно как полное урав­нение Букингама: .

> T(T-T0)dT = i^ri_-l_!o+ (И-24) о 8т|/ L 3 тс 3 тс У J

oJ^- > Г. ±

При т=& (du/dr)п (степенная жидкость) получаем

— Q = *R — > x2+^dx= ЛЛ*. (11.25)

* /я т® Зл 4-1 k )

Выражение (11.22) можно записать в виде

l— > T2/(T)dT. " (11.26)

я/гз i

— 4 . .

Такая запись выражения расхода диктуется тем обстоятельст­вом, что интеграл в (11.26) является функцией только своих пре­делов и поэтому величина Q/яЙ3 будет определяться только ве­личиной хс=Яр/21 независимо от вида реологической кривой /(т)~ Все точки на графике Q/яЮ—Яр/21 должны ‘ложиться на одну прямую. Если этого не произойдет, либо жидкость реологически нестационарна и ее характеристика зависит от времени, либо по­ведение течения аномально, либо происходит скольжение вблизи стенок трубы и тем самым нарушается основное условие инте­грирования, согласно которому и(Я)= 0.

Если рассматривать Q/nR3 как F(тс), то (11.26) можно пере­писать в виде

F(Tc) = -^]CT*fWdT (11.27)

тс О _

или

d [т^ F (тс)] = т2/ (т) dx. (11.28)

Решая (11.28) относительно /(т) с учетом пределов, получаем:

. 1 d [t|?F (тс)]

/(тс)-—г———— 2——— ‘• (п-29)

Тс dxc.

График зависимости тс = /Чтс) представляет собой кривую те­чения. Однако, как отмечает У. Л. Уилкинсон, хотя методика сама по себе правильная, но на практике кривая F(тс) часто оказыва­ется недостаточно крутой, чтобы дифференцирование в уравнении

(11.29) можно было осуществлять с требуемой точностью.

Раскрытие числителя выражения (11.29) по правилам диффе-

[ du

ренцирования с учетом, что F (тс) = Q/лЯ3, a f(xc) = — l • Дает:

=ig.+Tc, (11.зо)

dr J с лR3 dxc

Полученное уравнение известно в литературе как выражение Рабиновича и Муни для скорости сдвига на стенке трубы, не за­висящее от свойств жидкости, которая является реологически ста­ционарной. Если учесть, что

d (Q/nR3) „

и

j! F<L _ ^ in Х(. = d In (Rp/2l), тс

то выражение (11.30) можно привести к виду

3Q. dn(QfnR3)

TOC o "1-5" h z. dr )с лR3 +Qn dn(Rp/2l) ‘ ( ’ )

Однако чаще выражение (11.30) записывают несколько иначе, а именно, ‘ * .

(du 3 „ 1 din Г 3 /8о 1 /8о

— I 1 =— V 4- —тг ‘ ‘ ’ 1 ‘— 4

{du 3 „ 1 d In V 3 /8о 1 (8v Dj ‘

•где

(dr )с~ 4 + 4 VdlnTc_ 4 (d)+ 4 D/ dlnrc ( )

40 8n

V = ^ = v = W*Ri — <IL32a>

Обозначая логарифмическую производную в правой части (11.32) 1/п’, Метднер и Рид предложили более удобную форму записи выражения (11.32):

_fdu = Зя’ + 1 jl = ..3n, + l у (ПЗЗ

‘ dr Jс 4п’ D 4л v ‘

где

. d In %r dnT

(II.33a)

8и d In V

d In ■

D

T = xc = Rp/2ll. (11.336)

В практике реологических исследований выражение (П.26) ча­ще записывается в виде

V V = —l— ]^f(x)dx. (11.34)

4 T3 J0

Вместе с тем Метднер и Рид предложили взаимосвязь между V и Т выражать степенной зависимостью, аналогично формуле (11.10) Оствальда:

Т = kVn (11.35)

где k’ и п’ близки по своей сущности к величинам k и п в фор­

муле Оствальда.

Введение величин V и Т обусловлено тем обстоятельством, что графики V—Т, как отмечает Рейнер, не зависят от размеров при­боров и, следовательно, отражают определенное свойство испытуе­мого материала, которое получило наименование консистенции. Ве­личины V и Т называются консистентными переменными, а графи­ки в координатах V—Т — кривыми консистенции. .. .

По своей физической сущности величина Т представляет собой точную величину касательного напряжения на стенке трубы. Что касается величины V, то она имеет размерность градиента скоро­сти (скорости сдвига) й в литературе имеется несколько ее опре­делений: «средний градиент скорости», «градиент скорости сдвига у стенки» [61] и т. п.

Заметйм, что из выражения (11.33) отчетливо видно, что в об­щем случае величина V=8v/p сама по себе еще не градиент ско­рости; для того чтобы стать градиентом скорости, она должна быть дополнительно помножена на некоторую дробь, в которую входит показатель степени п’. .

Действительное выражение для градиента скорости найдем из уравнения Шведова — Бингама (11.12), заменив в нем т в соответ­ствии с (11.19): ,

(11.36)

du f гр * _1_ dr 21 Т°) г] ’

„ 1 В реологии для тс иведено обозначение Р. Однако в гидравлике буквой Р

обозначается обычно сила тяжести, а касательные напряжения принято обозна­чать через т или Т. Поэтому мы оставляем обозначение тс = Т.

или в случае, если r=R,

(11.37)*

Обратимся теперь к выражению (11.24). На основании выра­жений (11.19) и (11.37) после несложных преобразований его мож­но переписать в виде. ‘

Т£ = ^ + — Г-Г1-/-У1- (11.38)

dr nR3 3 Т] L тс / J

Из сравнения (П.32а) и (11.38) следует, что величина V может считаться градиентом скорости лишь с некоторым допущением и это следует иметь в виду при анализе кривых консистенции. Полу-

1

чающаяся при этом абсолютная погрешность Д — =——————— [1—(т,/тс)3Г

’ 3 т)

Если же исходить не из точного уравнения (11.24), а из приближен­ного (VI.22), широко используемого в практике, то, поступая ана­логичным образом, найдем, что в этом случае абсолютная погреш­ность a; = — jt0/ti. ‘ _

Если же в зависимости (11.38) принять то=0, то без каких-ли­бо допущений получаем, что,

-Ю — = — = V я/?3 dr ’

откуда следует, что величина V для случая ньютоновских жидко­стей представляет собой градиент скорости, найденный по значе­нию средней скорости при r=R. Наряду с этим для ньютоновской жидкости п’= 1 и из выражения (11.33) также йолучается, что в этом случае величина V точно соответствует скорости сдвига (гра­диенту скорости) на станке.

Аналогичные рассуждения можно применить и к жидкости, подчиняющейся степенному закону. ‘

Комментарии запрещены.