Бурение грунтовых зондов, установка энергетических колодцев

В самом общем виде кинетические закономерности любых про­цессов могут быть сформулированы в виде общего закона: ско­рость процесса прямо пропорциональна движущей силе и рбратно пропорциональна сопротивлению, которые необходимо преодоле­вать по мере осуществления процесса — будь то движение жидко — — — сти или газа, механическое движение или передача тепла. Называя величину, обратную сопротивлению, коэффициентом скорости [48], можно получить основные кинетические уравнения. Так, например, для движения потока промывочной жидкости или газа по каналам циркуляционной системы кинетическое уравнение будет иметь вид ;

(IH. I)

где V — объем протекающей жидкости; со — площадь сечения ка­нала; т—врем^; k — коэффициент скорости процесса; Ri — гид­равлическое сопротивление; Др — перепад давления.

Для движения (переноса) тепла кинетическое уравнение за­пишется в виде.

= k.2At;

(HI-2)

dQ At сodx R2

где Q — количество переданного тепла; со — поверхность теплооб­мена; т —время; k2 — коэффициент теплопередачи, т. е. величина, обратная термическому сопротивлению R2; At— средняя разность температур между средами, обменивающимися теплом.

Из равенств (III.1) и (III.2) вытекает, что для определения волной характеристики любого процесса помимо значения его ско­рости необходимо знать еще величины движущей силы и сопротив­ления. .Нахождение конкретных значений этих двух величин яв­ляется весьма сложной и трудоемкой задачей, без решения которой, однако, невозможно исследование процесса в целом.

Связь между средней скоростью v, общим гидравлическим дав­лением р, геометрической высотой (ординатой г) и потерями на­пора для любой точки потока жидкости устанавливается основным уравнением гидравлики, найденным Д. Вернули:

(Ш. З

где /ijs —так называемый дополнительный член, выражающий собой потерю напора (энергии) на преодоление гидравлических сопротивлений на пути между двумя какими-либо сечениями 1—1;

2— 2 потока; это и есть, величина движущей силы гидравлических процессов. В реальных условиях бурящейся скважины она опре­деляется как сумма напоров, расходуемых на преодоление гидрав­лических сопротивлений во всех звеньях циркуляционной системы. При этом потери напора разделяются на две категории: потери, вызываемые гидравлическими сопротивлениями по длине потока, hi и местные гидравлические потери hM, т. е. те потери, которые затрачиваются на преодоление тех или иных сопротивлений, не зависящих от длины (поворот, задвижка и т. п.). Очевидно, что в общем случае

hz = ht + hM. . (III.4)

Представление об Ti3MeHeHHii давления вдоль пути потока дает пьезометрическая линия, или линия давления. Так как, согласно уравнению Бернулли, давление зависит от скорости движения и может увеличиваться и уменьшаться в направлении движения в зависимости от того, уменьшается или увеличивается средняя скорость, пьезометрическая линия может в частных случаях иметь наклон вниЗ или вверх. Этим она существенно отличается от линии энергии, имеющей для реальных условий неизменное падение в сторону движения.

Под средней скоростью (точнее, средней объемной) v в задан­ном сечении со понимается некоторая фиктивная скорость, при которой вычисленный расход должен равняться действительному расходу жидкости Q, т. е.

v=Q/(в. <111.5)

При условии постоянства расхода для двух каких-либо живых сечений со 1 и ©2 такого потока должно быть справедливо соотно­шение, называемое условием неразрывности: ,

ffljt/, = ю2о2; =ю2<ог (III.6)

Если полную удельную энергию сечения умножить на вес жидкости, т. е. на уQ, получим энергию всей жидкости, протекаю­щей через это, сечение в единицу времени (обычно в 1 с), или мощность потока в этом сечении. .

Как обнаружил Кориолис, в реальных потоках имеет место неравномерность распределения скоростей по сечению. Для учета этого обстоятельства он предложил ввести в уравнение Бернулли коэффициент а: , ,

Pi Pi ^2

. zi+ у +“i 2g =Z2 + ~+a2 2g +h2′ ■ (I11’7*

При практических расчетах этим коэффициентом, как правило, пренебрегают, считая его равным единице, однако при неравно-

33

2 Зак. 1141
мерном движении погрешность из-за пренебрежения коэффициен­том Кориолиса-может оказаться значительной.

Следует помнить, что уравнение Бернулли можно использовать, только при условии, если рассматриваемая жидкость несжимаемая; капельная; движение рассматриваемого потока установившееся; выбранные сечения плоские и перпендикулярны к направлению движения; в этих сечениях давление распределяется по законам гидростатики, т. е. •

Р = Ро + *th> (III.8)?

где р — полное гидростатическое давление в рассматриваемой точке на глубине h под свободной поверхностью; р0— внешнее давление на свободной поверхности.

Величина движущей силы тепловых процессов определяется разностью температур сред, при наличии которой тепло распро­страняется от среды с большей температурой к среде с меньшей температурой. В условиях бурящейся скважины процессы пере­дачи тепла значительно усложняются тем, что здесь в зависи­мости от конструкции может быть не одна, а две или три колонны обсадных труб, расположенных концентрично или эксцентрично.. При этом число стенок (колонн), участвующих в процессе тепло­обмена, может меняться по глубине скважины.

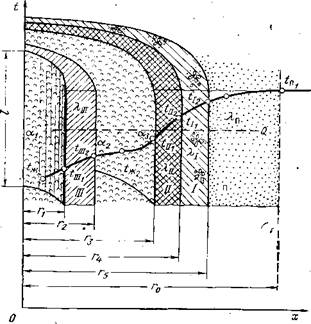
Однако, как было показано С. М. Кулиевым, Б. И. Есьманом и Г. Г. Габузовым, для выяснения принципиальных положений процесса теплоотдачи в бурящейся скважине вполне достаточна обойтись рассмотрением одного участка, поперечное сечение кото­рого показано на рис. 5. Согласно этой схеме предполагается,, что тепловой поток Q движется в направлении от породы Я к бу­ровому раствору Ж, находящемуся внутри бурильных труб III,. последовательно проходя через цементное кольцо I, трубы обсад­ной колонны II, восходящий поток бурового раствора ж2 и, нако­нец, стенки бурильных труб. III. При этом в каждом отдельном случае характер передачй тепла будет различным.

Так, процесс передачи тепла между непосредственно соприка­сающимися частицами, имеющими различную температуру, проис­ходит в результате теплопроводности или кондукции *, причем в’чистом виде процесс теплопроводности наблюдается в твердых телах и в тонких неподвижных слоях жидкости или газа.

Между движущимися частицами жидкости или газа тепло пе­редается вследствие конвекции[9], причем конвекция всегда сопро­вождается кондукцией. , —

Тепло может передаваться и тепловым излучением (радиация).

Обычно наблюдаются одновременно все виды теплообмена и разграничить их действие затруднительно’. Поэтому один из них, превалирующий в рассматриваемом случае, принимается за основ—

ной, а влияние остальных учитывается соответствующими поправ­ками.

Процесс передачи тепла при соприкосновении движущейся жидкости со стенкой называют теплоотдачей. Если же тепло от одного теплоносителя к другому йередаётся через разделяющую их преграду, то такой сложный процесс называется теплопередачей.

‘Рис. 5. Схема передачи тепла в поперечном сечении бурящейся скважины

Тепло может распространяться при установившемся (стацио­нарном) или неустановивщемсд (нестационарном) режиме. При этом под установившимся тепловым режимом понимается такой тепловой процесс, при котором температура t в каждой точке остается во времени т постоянной, т. е. при таком процессе произ­водная dt/dт равна нулю. Если dt/dx отлична от нуля, то имеет место неустановившийся тепловой режим.

Согласно закону Фурье о распространении тепла путем тепло­проводности, количество передаваемого тепла Q за промежуток времени т через поверхность F выражается уравнением

Q = — XF т —= —XF т— (III.9)

п • п

или в дифференциальной форме

dt

dQ = — X —— dFdx, (ШЛО)

on

где Я — коэффициент теплопроводности; п — толщина слоя; tCt w tCt — температуры на поверхности стенки соответственно со сто­роны входа и выхода теплового потока. Знак минус указывает на то, что с увеличением толщины стенки температура убывает. Тем­пературный градиент dt/dn определяется из выражения ’

TOC o "1-5" h z lim At dt

a nr==7 = ^adi’ (III.11>

Д п-+ ОД п дп

Очень часто расчеты ведутся по отношению к удельному тепловому потоку q. В этом случае ■

О dt

-А/— . (Ш.12>

Fт дп

При решении задач, связанных с конвективным теплообменом, основной является формула, вытекающая из закона теплообмена Ньютона: , г,

Q = aF (tc — *ж) = aFAt ‘ (III. ia>>

или в дифференциальной форме

• dt

dQ = a—- dFdx, (III.14>

дп.

iae F — площадь теплообмена; tc — 1Ж—- разность температур (температурный напор) между стенкой и соприкасающейся с ней жидкостью; а — коэффициент теплоотдачи.

Коэффициент теплоотдачи показывает, какое количество тепла передается от соприкасающейся среды единице площади стенки^ при температурном напоре, р’авном 1 °С,

Комментарии запрещены.