Бурение грунтовых зондов, установка энергетических колодцев

Рассмотрим теплопроводящий стержень, торцы которого имеют различную те пературу — Тн и Тс Очевидно, что в этом случае с одного торца в стержень бу л ВХОДИТЬ некий тепловой ПОТОК МОЩНОСТЬЮ Рнр, а с другого торца из стержня б 1. ВЫХОДИТЬ тепловой ПОТОК МОЩНОСТЬЮ Рср. Если боковая поверхность стержня IUB ально теплоизолирована, то тепловой поток через нее отсутствует, и

РНF = PCF = ^(Рн~ Р()- 1 Ч

В формуле (1) Л — теплопроводность стержня, Вт/К, в системе СИ, А = (А/і) «I где А — площадь сечения стержня; / — его длина; К— коэффициент теплопрв водности, Вт/К в системе СИ. Индекс F в обозначениях принят в связи с те что явление теплопроводности иногда называют эффектом Фурье в честь Же Баптиста Жозефа Фурье, тем самым отмечая его вклад в изучение процессе* рассеяния тепла.

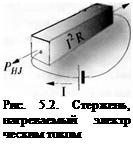
Теперь предположим, что стержень имеет одинаковую по длине фиксирован-! ную температуру, но за счет нагрева посредством электрического тока его темпер ратура выше, чем температура тел, которые соприкасаются с торцами стержні. В этом случае тепловой поток будет выходить из стержня. Тепловая мощное I выделяющаяся в стержне вследствие протекания электрического тока, равна R! где R — электрическое сопротивление стержня. При этом половина выделивше-1 гося тепла будет уходить через один торец стержня и половина через другой:

рш= ра= 1/2К/2. (2І

Индекс /указывает на то, что выделение тепла в стержне обусловлено эффектен Джоуля (Джеймс Прескотт Джоуль). Заметим, что направления тепловых поток >« на рис. 5.1 и 5.2 различаются. Если за направление теплового потока выбрать ис­правление, указанное на рис. 5.1, то поток //убудет отрицательным.

Если представить себе, что вдоль стержня имеется градиент температуры > через него протекает электрический ток, то мы будем иметь суперпозицию эф фектов Фурье и Джоуля:

Здесь в качестве положительного направления теплового потока выбрано Управление, указанное на рис. 5.1. Однако в более сложных конструкциях на — ,■явление теплового потока может быть довольно неожиданным.

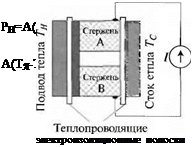
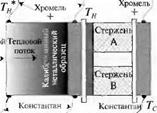
Рассмотрим термопару, состоящую из двух различных по свойствам мате — юв (проводников или полупроводников), соединенных один с другим. Эти сриалы (стержни А и В на рис. 5.3) могут непосредственно соприкасаться, ■ і могут быть соединены с помощью металлической пластины, как показано рисунке. До тех пор. пока металлическая пластина имеет постоянную темпе — уру, она не оказывает никакого влияния на характеристики термопары (пред — ндгается, что электрическим сопротивлением пластины можно пренебречь, а ; тешюпроводность практически бесконечна). Свободные концы стержней А В подсоединены к источнику тока.

Рис. 5.3. Простая термопара (слева) и тестовая конструкция (справа)

Если соединительные провода имеют постоянную температуру, то они также оказывают никакого влияния. Пусть место контакта (спай) двух материалов, ‘дкже их свободные торцы термически связаны с двумя тепловыми резервуа — и. которые имеют постоянную температуру. Резервуар, соприкасающийся спаем материалов, является источником тепла (далее нагреватель), и его ■ пература Тн — Другой резервуар является поглотителем тепла (далее холо — зьник), и его температура Тс. Будем считать, что нагреватель и холодиль — ■, электрически изолированы от термопары. Способ измерения мощности лового потока Р№ идущего от нагревателя к холодильнику, будет описан конце этого параграфа.

Представим, что термопара теплоизолирована от окружающей среды, так что может обмениваться теплом только с нагревателем и холодильником. Если

измерить зависимость Рн от (Тн — Тс) в случае отсутствия электрического ток через термопару, то окажется, что величина РИ пропорциональна разности тем­ператур (см. уравнение (1)):

РН=А{ТН-ТС). (-J|

Взяв в качестве примера Л = 4,18 Вт/К, получим

РЯ=4,18(ГЯ — Тс). (61

Если через термопару, обладающую электрическим сопротивлением R, про-| текает электрический ток /, то согласно уравнению (3)

РН=А(ТН- Тс)~ 1/2 RP, Г

или если сопротивление термопары R = 2,6 ■ 10-4 Ом, то

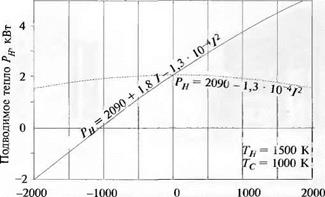
Рн= 2090 — 1,3 • 10-4/2. (8.

В (8) мы, в качестве примера, приняли, что Тн= 1500 К и Тс= 1000 К.

Ток I, А Рис. 5.4. Зависимость между мощностью подводимого теплового потока Рн и сил’ Ч тока I для термопары

Полученная зависимость Рн от / показана на рис. 5.4 штриховой лини:

В действительности оказывается, что значение РИ зависит не только от тока, на и от его направления. Экспериментально определенная зависимость Рн от I д. Я некоторой термопары представлена на рис. 5.4 сплошной линией. Данная зави­симость хорошо описывается полиномом второй степени:

Рн= 2090 + 1.8/- 1,3 • 10-4/2. (9»

Первый член в уравнении (9) описывает теплопроводность и не зависит пі значения тока. Третий член описывает джоулев нагрев 1,3 • 10-4/2. Кроме того, в уравнении (9) имеется член, пропорциональный значению тока I.

Из этого следует, что если ток течет в одном направлении и тепловой поток правлен от нагревателя к холодильнику, то при перемене направления тока изменится и перенос тепла. Очевидно, что электрический ток переносит тепло — ю энергию. Явление обращения переноса тепла называется эффектом Пельтье їЖан Шарль Асанас Пельтье, 1785-1845).

Эмпирически установлено, что перенос тепла, обусловленный эффектом рельтье, пропорционален силе тока, т. е. можно записать

^Peltier = 71 ^ (Ю)

. к — коэффициент Пельтье.

Если к термопаре вместо генератора тока присоединить идеальным вольтметр, можно измерить зависимость получаемой электродвижущей силы (ЭДС) Vот ности температур нагревателя и холодильника АТ = Тн- Тс Эта зависимость тется нелинейной. На рис. 5.5 представлена зависимость ЭДС термопары от іературьі нагревателя Тн в предположении, что температура холодильника Тс ерживается постоянной и равной 173,3 К1′.

Коэффициент Зеебека а определяется как тангенс угла наклона кривой V от »: слабо зависит от температуры

В дальнейшем мы покажем, что связь между коэффициентами Зеебека Пстьтье выражается соотношением:

л = аТ.

О-7

или, если принять среднее значение коэффициента Зеебека равным <а>, то

V=<a>{ТН — Тс).

В дальнейшем в этой главе мы, подразумевая среднее значение коэффициент <а>, будем записывать его просто как а. Пользуясь средним значением коэфф. н циента Зеебека а, мы можем достаточно точно описать рабочие характеристика термопары, основываясь только на четырех вышеописанных эффектах, а именно: Фурье, Джоуля, Пельтье и Зеебека, и полностью пренебрегая эффектом Томсон Справедливость такого подхода будет обоснована в конце главы.

Точность измерения температуры тела с помощью термопары (рис. 5.5) определяется классом вольтметра, измеряющим ЭДС термопары (средний вольтметр имеет погреш­ность измерения около 0,1 % полной шкалы). Точное определение теплового потока является более сложной задачей.

Теплове

поток

Рис. 5.6. Схема измерения теплового потока в термопару

В принципе тепловой поток можно организовать путем пропускания электрического тока через резистор. Естественно при этом не должно быть электрического контак та между термопарой и источником тепла. В этом случае электрическая мощность необходимая для поддержания постоянного значения температуры, является мерой теплового потока от нагревателя к термопаре.

Обычно для измерения теплового потока используется металлический образец (предпо­лагается, что зависимость его удельной проводимости от температуры хорошо известна), который располагается между источником тепла и термопарой. Если тепловые потери через поверхность образца отсутствуют, то тепловой поток в термопару может быть рассчитан исходя из падения температуры (Тн* ~Тн) вдоль металлического образца Температуры Тн* и Тн так же, как и температура Тс, измеряются дополнительными термопарами, которые соприкасаются с соответствующими местами устройства.

Термопары находят применение в следующих устройствах:

1) термометрах

2) прямых преобразователях тепловой энергии в электрическую;

3) тепловых насосах и холодильниках.

Комментарии запрещены.