Бурение грунтовых зондов, установка энергетических колодцев

Распределение электронов в металлах не является максвелловским распределением. Электроны подчиняются принципу запрета Паули, согласно которому в заданной системе не может быть двух электронов, имеющих одина­ковые квантовые числа, и, следовательно, все электроны не могут иметь нулевую энергию при абсолютном нуле. Точнее, при абсолютном нуле электроны должны быть равномерно распределены по энергиям вплоть до некоего заданного уровня энергии. Электрон не может иметь энергию, превышающую этот энергетический уровень, называемый уровнем Ферми. В этом случае вероятность нахождения электрона на некоем данном энергетическом уровне равна:

/ = 1 при W < WF и /= 0 при W > WF

Как и раньше, число разрешенных состояний с импульсом, меньшим р (об — рашаем внимание на изменение терминологии), пропорционально объему сферы v радиусом р в пространстве импульсов:

е^ь величина 2/И3 является коэффициентом пропорциональности. Не вдаваясь детали, отметим, что множитель 2 является следствием наличия у электрона л возможных состояний, отличающихся спиновым числом, а размерность ве гствует тому, что N— число электронов в 1 м3.

Так какр = mv, то р2 = 2mWvi

(92)

Тогда

Э W

При температуре больше нуля вероятность того, что некое данное энергети — ое состояние занято, выражается как

Величина р называется химическим потенциалом. При Т= 0, р — WF и ве — ность/= 1 при W< WFи/= 0 при W> Wp как это и требуется. При Т ф О ина р немного меньше WF.

Используя функцию (94), можно найти плотность состояний

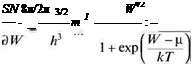
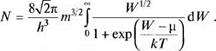(95)

(96)

тдк как N не зависит от Т, то интеграл также должен не зависеть от Т. Из следует, что химический потенциал р должен зависеть от Т неким опре — шм образом. кТ« р

интеграл не зависит от Т, а р = WF.

При более высоких температурах, для того чтобы быть уверенным в инвари­антности интеграла, необходимо, чтобы р зависело от Т приблизительно, как в выражении

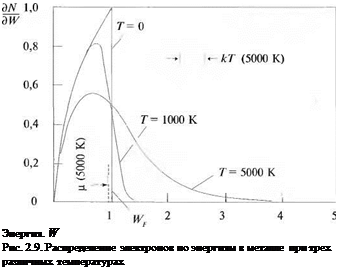Разница между р и WF незначительна. Для уровней Ферми с энергией от 5 эВ при температуре порядка 2000 К она составляет только 0,1 %. Поэто­му для большинства приложений химический потенциал может быть принят равным энергии уровня Ферми. Одно исключение из этого правила имеет место при рассмотрении термоэлектрического эффекта. На рис. 2.9 показа­ны зависимости плотности состояний dN/d W от Wдля трех значений темпе­ратуры. Отметим, что химический потенциал, который совпадает с уровнем Ферми при Т = 0, при более высоких температурах сдвинут в сторону более низких значений.

2.18. ЗАКОН БОЛЬЦМАНА

Весьма важным законом, вытекающим из статистической ме­ханики, является закон Больцмана, который описывает концентрацию частик в газе как функцию их потенциальной энергии и температуры. Этот закон ис­пользуется в различных главах этой книги.

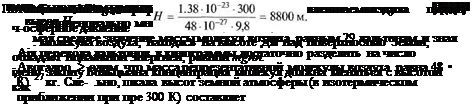П сть на каждый атом действует потенциальная сила Г, направленная вдоль и х. Тогда nF представляет собой полную силу, действующую на 1 м3 газа. Если ограничим себя рассмотрением прямоугольного параллелепипеда с плошадью нования А и высотой dx, то сила будет равна nFAdx и соответственно давле­на основание будет равно nFcbc. В равновесии это давление должно быть новешено давлением газа kTdп.

ПРИЛОЖЕНИЕ

Комментарии запрещены.