Бурение грунтовых зондов, установка энергетических колодцев

На частицу шлама, падающую в жидкости (газе), действуют сле­дующие силы:

— лобового сопротивления:

^л. с = 0,5СлсУшРи2; (5.40)

— подъемная (Архимеда):

Fm = mgЈ~; (5.41)

Г ш

— тяжести:

FT = mg, (5.42)

где Слс — коэффициент силы лобового сопротивления; /ш — площадь

речения частицы шлама, м2; р — плотность жидкости (газа), кг/м3;

рш — плотность частицы, кг/м3; v — скорость шлама относительно сре­ды, м/с; g — удельная сила тяжести (ускорение свободного падения), Н/кг; т — масса частицы, кг.

Падение частицы является ускоренным. Тогда уравнение движе­ния частицы будет следующим:

(5.43)

где / — время падения, с; 5—путь шлама, м.

Подставляя (5.40) — (5.42) в (5.43) после интегрирования получим

где ув — предельное недостижимое значение скорости шлама отно­сительно жидкости, м/с; ^ — эквивалентный диаметр частицы шла­ма, м; /А (х) — гиперболический тангенс.

Под эквивалентным диаметром частиц шлама понимают диаметр ча­стицы шлама, имеющей тот же объем, что и у наиболее крупных частиц.

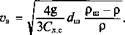Эквивалентный диаметр частицы соизмерим с выпуском подрез­ных резцов коронки или с шагом зубьев шарошечного долота. При бурении зернистых пород эквивалентный диаметр может быть соиз­мерим со средним размером зерен породы.

(5.45)

Скорость падения шлама относительно среды согласно (5.44) все время возрастает. Лишь в пределе при t -> °° (или v —>vB = const.

Однако при оценке условий выноса шлама по стволу скважины пользоваться строгим решением (5.44) неудобно. Как правило, в бу­ровых гидравлических расчетах промывки (продувки) с целью их упрощения вводят условное понятие «скорость витания» vB (гидрав­лическая крупность).

Под скоростью витания понимают условную скорость равномер­ного падения тела в неподвижной неограниченной жидкости (газе). Если восходящему потоку придать скорость витания, то тело зависнет в потоке, т. е. будет витать.

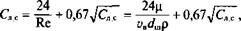Рассмотрим равномерное падение шлама в ньютоновской жидко­сти (газе). В этом случае уравнение (5.45) называют формулой Рит — тингера. Величина коэффициента Слс при докризисном обтекании (именно оно характерно для процесса падения шлама) точно описана А. Д. Альтшулем опытной формулой

(5.46)

где ц — абсолютная вязкость жидкости (газа), Па • с; Яе — число Рей­нолдса при обтекании шара.

Для определения величины Слс при падении шлама в бингамов — ской жидкости (глинистом растворе) применяют опытные формулы,

полученные для случая падения шлама в ньютоновской жидкости (газе), если в последние вместо числа Рейнольдса (Яе) подставить мо­дифицированный критерий Рейнольдса:

Яе

Яе* =

(5.47)

1 +

где т0 —начальное напряжение сдвига жидкости (газа).

Решая совместно (5.45) и (5.46) и применяя замену Яе на Яе* по (5.47), после преобразований получим:

36ц

+ 0,67

^■5УзРё(Рш — р) , 6х0

С = ‘"•’Л. С

(5.48)

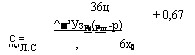(рш Р)

Выражение (5.48) справедливо как для НЖ (газов), так и для БЖ. Однако в отличие от НЖ не во всякой БЖ будет тонуть тяжелая (рш>р) частица шлама. Приравнивая сумму подъемной силы Архиме­да (5.41) и силы трения на поверхности шара величине силы

тяжести (5.42), получим, что частица шлама будет тонуть в БЖ при выполнении неравенства

6т0 < 8^ш(рш — р). (5.49)

Только в этом случае справедливы решения (5.45) и (5.48). Если

6т0 > — р),

(5.50)

то частица шлама перемещаться относительно БЖ не будет, величи­ны Сдс не существует, ив = 0.

Следует иметь в виду, что частица шлама, находящаяся вблизи оси потока (где скорость выше), может выноситься на поверхность со скоростью, большей, чем средняя скорость потока.

Комментарии запрещены.