ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О ТЕМПЕРАТУРНОМ РЕЖИМЕ СКВАЖИН ПРИ БУРЕНИИ
ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О ТЕМПЕРАТУРНОМ РЕЖИМЕ СКВАЖИН ПРИ БУРЕНИИ
Результаты исследований процессов тепло — и массопереноса в бурящейся скважине [40, 65, 68] показали, что дальнейшее их изучение целесообразно проводить как в направлении упрощения общей постановки задачи о ее температурном режиме для нахождения замкнутого приближенного решения в аналитическом виде или с помощью ЭВМ, так и путем перехода к исследованию отдельных частных случаев с более полным отражением основных деталей реальных физических явлений, происходящих в отдельных частях системы скважина — массив горных пород. В первом случае структурный анализ решения общей задачи открывает новые возможности для нахождения приближенных зависимостей распределения температуры в скважине с учетом конкретных условий бурения. Во втором случае при сохранении некоторых
основных особенностей, характеризующих процессы тепло — и массо — переноса в бурящейся скважине, появляется возможность рассмотреть влияние того или иного фактора, участвующего в формировании температурного поля в скважине, на каком-либо конкретном примере, которому может соответствовать более простая математическая модель.
Рассмотрим общую задачу о температурном режиме бурящейся скважины. С целью упрощения полученной в предыдущем разделе ее общей математической модели воспользуемся осевой симметрией исследуемой системы и перейдем к цилиндрическим координатам, совместив ось 2 с осью скважины и направив ее вертикально вниз, а за начало координат взяв точку пересечения оси скважины с горизонтальной плоскостью, проходящей через ее устье (см. рис. 1.12).
В области I, занятой промывочной средой, как это показано в работах ’[40, 46], достаточно знать лишь усредненные по сечению каналов значения скорости, давления и температуры в циркулирующем потоке среды. Тогда из общих уравнений (1.17), (1.18) и (1.20), отмечая параметры потока во внутреннем канале бурильной колонны индексом 1, а в кольцевом канале индексом 2, с учетом проведенных в работе [40] исследований получаем следующие уравнения для определения средних по сечению каналов величин:
|
( <?(р, М, <30,
|
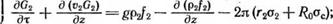
|
2ла2 (г2о2 + /?(1Ос) = <?2 — <71- |
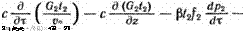
|
(1.29) |
![]()
|
Здесь С — массовый расход; f — площадь сечения канала; с — удельная теплоемкость среды; V — скорость потока промывочной среды; р — коэффициент объемного расширения среды; г2 — внешний радиус бурильной колонны; а, сг2 и ос — касательные напряжения на внутренней и наружной стенках бурильных труб и на стенке скважины; q и <72 — тепловые потоки через бурильные трубы и на стенке скважины. Тепловой поток в единицу времени через стенку бурильных труб, отнесенный к единице длины, может быть определен из условия теплообмена по закону Ньютона (граничное условие |
 д(РгЫ. дС, — дх ‘ дг
д(РгЫ. дС, — дх ‘ дг
третьего рода) в виде выражения
<7, = 2пгх1г (/2 — /,), (1.30)
где А: = (1 /«1 + бтДт + 1/аг)-1 — коэффициент теплопередачи через стенку бурильной трубы толщиной бт; Я, т — коэффициент теплопроводности материала трубы; <ц и а2— коэффициенты теплоотдачи на внутренней и внешней поверхностях бурильной трубы.
Аналогично находим выражение для теплового потока на стенке скважин
— 2я/?оас |г=д0 4). (1.31)
где ас — коэффициент теплообмена на стенке скважины; tn |г==/?( —
■температура пород на стенке скважины.
Для замыкания системы уравнений (1.28) — (1.29) ее необходимо дополнить уравнением состояния, связывающим давление, плотность и температуру среды. Для однозначного определения искомых параметров среды необходимо также задать начальные и граничные условия, которые в нашем случае могут быть сформулированы следующим образом:
а) т = т0; = й(2); г2 = $ (г); р, = р?(г); р2 = р%(г);
б) 2 = 0; /, =*1н(т); р! = р1н(т); б, = (т); 0-32)
в) 2 = //; = р2 — р1~~^рз> 62 = + ДС3.
Условие (1.32а) определяет закономерность распределения параметров промывочной среды по глубине скважины в начальный момент времени. Предполагается, что эта закономерность известна или задана.
Условие (1.326) является условием на устье скважины при входе промывочной среды в бурильную колонну и выражает тот случай, когда температура, давление и расход промывочной среды заданы. При замкнутой системе циркуляции на устье скважины, как правило, известна разность температур Д? у = £у2— Iуц поэтому условие (1.326) в этом случае принимает вид
2 = 0; г, = г2 + Д/у; р2 = ру(т); <?1 = С( т).
Условие (1.32в) представляет собой математическое описание условий на забое скважины. Здесь £3 — повышение температуры промывочной среды в зоне забоя за счет источников тепла, связанных с работой породоразрушающего инструмента или забойного двигателя; Др3 — перепад давления промывочной среды в зоне забоя; Д(?3 — изменение расхода промывочной среды в зоне забоя скважины за счет возможных ее утечек или притоков к ней флюидов из горного массива.
В условиях (1.326) и (1.32в) Д/у, Д*3, Дрз, ДС3 определяются процессами тепло — и массопереноса, происходящими в третьей и четвертой частях рассматриваемой нами области (см. рис. 1.12).
Если температура стенки скважины известна, то система уравнений (1.29) —(1.31) с условием (1.32) становится замкнутой.
В общем случае температура tn |r=J? не известна и определяется условиями переноса тепла в области II из уравнения (1.26), которое в цилиндрических координатах принимает вид
РЛ,^-Н (V-f-) +£г (к&) (1-33)
для /? г оо; 0 ^ 2 ^ Я; т > 0.
Начальные и граничные условия для уравнения (1.33) могут быть записаны в виде
а) T = to; *„ = №’» H = Hv
б) 2 = 0, ^п==^по(т)і
в) 2 = Я; Ап a^„/az = а3 (/„ — /3); (1.34)
г) r==^0; Ап dtjdr = ас (fn |г=Ло — fa);
д) г —> оо; f ^* (z) —> 0.
Здесь f„(z) — распределение начальної“! температуры пород по глубине; t„o — температура пород на поверхности земли; а3 — коэффициент теплообмена между промывочной средой и забоем скважины; t3 — температура промывочной среды на забое скважины.
В период простоя скважины и отсутствия теплообмена с массивом горных пород уравнение (1.33) с условиями (1.34) описы
вает температурное поле пород горного массива, при этом
Я = const; ас = «з = 0.
Полученная система уравнений (1.28) — (1-32) и (1.33) с условиями (1.32) и (1.34) значительно проще исходных, однако решение и этих уравнений возможно в общем виде только численными методами. Принимая во внимание особенности изучаемого процесса, можно продолжить упрощение математической модели нашей задачи, пренебрегая в полученных уравнениях слагаемыми, которые не оказывают заметного влияния на точность решения. В работах [40, 68] обоснованы следующие дополнительные предположения, которые могут существенно упростить математическую формулировку исследуемой задачи и ее последующее решение:
а) движение потока промывочной среды установившееся, т. е. его расход и давление не зависят явно от времени;
б) распределение температуры в стенке бурильных труб подчиняется линейному закону по г,
в) теплота в окружающем скважину горном массиве распространяется только в радиальном направлении;
г) сечение циркуляционных каналов не меняется по глубине скважины;
д) изменением физических и теплофизических характеристик промывочной среды по глубине скважины можно пренебречь.
Тогда с учетом вышеперечисленных упрощений и дополнительно выполненных преобразований, математическая модель задачи о температурном режиме бурящейся скважины примет вид
а) (1/t;,) dtjdт — f dtjdz — f — е, (2) — q = 0;
б) (1/tg dtjdr — dt2/dz + e2 (2) + q" — q2 = 0;
в) d(pifi)/dz = gPifi — 2nrlali
|
Здесь |
![]() Г) d (p2f2)/dz = —gp2f2 + 2я (r2a2 + R0ac)
Г) d (p2f2)/dz = —gp2f2 + 2я (r2a2 + R0ac)
д) Gi = G = const; G2 — G, + AG3 = const.
|
2я/?0ас ,, |
|
G2c V" »■=«о i 2nr, vlot |
|
г С(с ’ 2jto2 (г2с2 + RqQc) G2c |
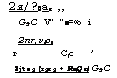 |
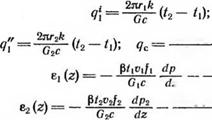
61(2) и 62(2)—изменение температуры в циркуляционных потоках промывочной среды за счет ее объемного расширения и трения при движении о стенки канала.
Начальные и граничные условия:
а) т = т0; /, = /?(г); t2 = & (2);
б)2 = 0; il = t[R(x) или /, = г2 + Л/у; р, = р„ (т); (1.36)
в) 2 = Я; t2 = ti+ А/3; р2 = р, + Ар3.
Расчетный анализ величин, характеризующих изменение теплоты в циркуляционных потоках за счет объемного расширения среды и преодоления сил трения при движении о стенки каналов 61(2) и £2(2), проведенный в работе [40], показывает, что их влияние на изменение температуры среды в потоке взаимно противоположно. По абсолютным значениям для конкретных условий разведочного бурения это часто величины одного порядка, не выходящие за пределы погрешностей, связанных с расчетом основных характеристик циркуляционной среды. Поэтому с достаточной для наших расчетов точностью учетом влияния этих слагаемых можно пренебречь, считая ei (2) = e2(z) = 0.
При использовании в качестве промывочной среды несжимаемой ЖИДКОСТИ, Т. е. р| = const, р2 = const, в случае постоянного массового расхода среды Gi = const гидродинамические параметры в системе уравнений (1.35) становятся известными и задача определения температурного поля в скважине оказывается самостоятельной. Для ее исследования необходимо только рассмотреть совместно уравнения переноса энергии промывочной среды в бурильной колонне и в кольцевом канале скважины с уравнением
теплопроводности, описывающим процесс переноса тепла в окру — жающих скважину горных породах.
Если в качестве промывочной используется сжимаемая среда (воздух, газожидкостная смесь), то система уравнений (1.35) применима только для случая установившегося в скважине квазиста — ,
ционарного режима теплообмена, когда и д^2/дт-*-0.
Рассмотрим подробнее распределение температуры в потоках циркулирующей промывочной среды для случая бурения скважины. С этой целью перейдем в системе уравнений (1.35) к безразмерным переменным, определив предварительно следующие характерные параметры: Я = Я0 + им(т— то)—изменение глубины скважины в процессе бурения; Но— глубина скважины к началу процесса (цикла) бурения скважины; юи — средняя механи — <
ческая скорость бурения (скорость перемещения забоя скважины);
-Го — начальный период, связанный с промывкой скважины без <
углубки забоя; Я* = Н0 + ^мТ№ — характерная глубина скважины в процессе бурения; т* — характерное время проходки (продолжительность рейса, цикла); ДЯ = Я*— Но-—абсолютное углубление скважины в процессе бурения.
Будем считать, что начальное распределение температуры в скважине совпадает с геотермическим, т. е.
где Г — геотермический градиент температуры; ід — температура
нейтрального слоя.
Тогда в качестве характерной температуры в скважине можно принять, например, при глубоком бурении = ГЯ*, а в
случае бурения мелких скважин температуру нейтрального слоя
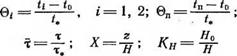
|
и перепишем уравнения (1.35а) и (1.356) в безразмерном виде: |
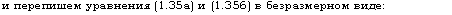
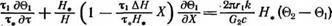
|
т2дв2 Я» /. , Т2ДЯ дв2 т„ дг Н V т, Н Л) дХ |
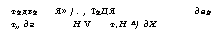
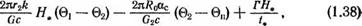 Введем обозначения для безразмерных величин
Введем обозначения для безразмерных величин
где т, ==Я*/иг — время, за которое частица жидкости пройдет от устья к забою и обратно.
Анализ полученных уравнений показывает, что если множитель тг/т, 1, то соответствующие слагаемые в уравнениях можно без ущерба для точности нашего решения отбросить. Таким образом.
если характерное время рассматриваемого процесса бурения значительно больше времени прохождения элементарного объема промывочной среды от устья скважины до ее забоя, то в уравнениях (1.37) и (1.38) можно не учитывать слагаемые, характеризующие скорость изменения температуры от времени, и составляющую конвективного переноса теплоты за счет перемещения забоя вдоль оси г в процессе углубки скважины. Кроме того, конвективный перенос тепла за счет перемещения забоя можно не учитывать и при сравнительно небольших углубках скважины по сравнению с ее характерной глубиной, когда кИ ^ Ищ. Условие малости вышеупомянутых слагаемых очевидно будет выполняться всегда, когда изменение температуры во времени незначительно или носит плавный характер.
Так как все эти условия характерны для установившегося ква — зистационарного процесса бурения, являющегося основным технологическим режимом бурения разведочных скважин различной глубины, в дальнейшем ограничимся рассмотрением только таких случаев.
Учитывая вышесказанное, температурное поле в бурящейся скважине можно определить системой уравнений
1 «30, _ 2пг, к ^ 39^
|
:[2^1(02_@1)_ 2я^ас.(02_0п)]я + £Н_ (1.40) (1.41) |
Кн дХ
с начальными и граничными условиями
X = 0, 0, = 0Н или 0] = 02 + Д0У;
*=1, 02==01 + Д0з;
где
К —
0 = —5 4-. Д0 = 1.. Д03 = —2. .
иН 4 » аиу * » * /
*■# *■# 1«,
Уравнения (1.39) и (1.40) с соответствующими начальными и граничными условиями (1.41) полностью определяют распределение температуры в бурящейся скважине, как это уже отмечалось выше, только при известной температуре стенки скважины 0с, которая является в свою очередь результатом теплового воздействия потока промывочной среды в кольцевом канале скважины на массив горных пород, а поэтому должна быть определена решением задачи о переносе тепла в области //, представленной на схеме нашей задачи (см. рис. 1.12).
Рассмотрим для этой области уравнение переноса тепла в безразмерном виде. Для этого перейдем к следующим безразмерным переменным
TOC o "1-5" h z £ __________ _____ г
й ___ _5 Л — /? — ■
п~ К ’ «о’
— Яп / *£ — Яп
Ро = Ро = — -^(т0 +————————— М; К,
спРп^0 °м )
где Fo = ^пт/(спРп^о) ~ критерий Фурье (безразмерное время); сп и — характерные значения теплоемкости и теплопрородности пород.
Тогда уравнение переноса тепла в горных породах примет вид
дв„ 1 д ( двЛ Rl д С двЛ
Так как для скважины Ro ^ Н, то переносом тепла в горных породах вдоль оси г можно пренебречь, и уравнение (1.42) значительно упрощается
(1-43)
Начальные и граничные условия для уравнения (1.43) могут быть записаны в виде
а) Fo = 0, ©п = 0;
б) R= 1, К,^ = ас (0П |л_, — 02); (1.44)
в) R-* оо, 0„->О,
где ас — безразмерный коэффициент теплоотдачи.
При отсутствии в породах фазовых переходов анализ точного, но довольно сложного решения уравнения (1.43) с условиями
(1.44) , приведенный в работах [11, 40, 68], позволил обосновать возможность использования для расчета температурного режима бурящейся скважины с необходимой для практических целей точностью понятия о коэффициенте нестационарного теплообмена, который определяется следующим соотношением [III:
0.4Б)
Идея основана на предположении о том, что производными по времени в уравнениях теплопереноса можно пренебречь, а неста — ционарность процесса учесть специальным поправочным коэффициентом kr, определяя с его помощью тепловой поток на стенке скважины следующим образом:
В работе [23, 40] рассмотрены точные и приближенные методы определения kx при известных значениях коэффициента теплоотдачи в кольцевом зазоре скважины ас. Для определения kT предлагается зависимость
6t = acq)(Fo), (1.47)
где cp(Fo) может быть вычислена как по точным, так и по приближенным формулам, учитывающим возможность определения среднего и среднеинтегрального значения kx как по времени бурения, так и по глубине скважины.
С помощью понятия о коэффициенте нестационарного теплообмена kx связь между температурой стенки скважины и температурой циркулирующей среды в кольцевом канале может быть определена в безразмерном виде следующим выражением:
©п1«=1=(1-^/ас)02. (1.48)
Необходимо отметить, что с помощью коэффициента нестационарного теплообмена kx можно рассчитать температуру только после наступления квазистационарного режима теплообмена в скважине.
На основании анализа и упрощения общей математической модели процессов тепло — и массопереноса в бурящейся скважине получена система двух уравнений, описывающая изменение температуры циркулирующей в скважине промывочной среды.
При условии отсутствия в скважине утечек промывочной среды и притоков к ней флюидов из горного массива, т. е. при Gi —
— 62 — G — const, при отбрасывании производных по времени и использовании понятия о коэффициенте нестационарного теплообмена kx, уравнения (1.39) и (1.40) с учетом равенства (1.48) могут быть преобразованы к виду
d®t/dX — а (02 — ©,) + Г0 = 0; (1.49)
дв2/дХ + а (02 — ©,) — f bk%( — Г0 = 0 (1.50)
SHAPE \* MERGEFORMAT 
при следующих граничных условиях:
|
(1.51) |
![]() а) X = 0, 0! = 0„ или 01 = ©2 + А©у;
а) X = 0, 0! = 0„ или 01 = ©2 + А©у;
б)х = , ©2=©, + а©3,
где
2л/-(йК„Я 2я R. K. „Н
а ————- — • Ь ———— —-—:
а Ос ‘ и Ос
ГН
|
о ■ |
![]() Т,
Т,
Поставленная задача в упрощенном виде сводится к решению системы, состоящей из двух линейных однородных дифференциальных уравнений с двумя переменными ©1 и 02. Для решения
данной системы из первого ее уравнения (1.49) определим @2, и
полученное выражение подставим в уравнение (1.50). После ряда преобразований приходим к следующему выражению для распределения температуры в канале бурильной колонны:
~ (а + ЬкЛ = 0 (1 ‘52)
с граничными условиями
а) X = 0, ©1 = ©2 или ©1 = ©2 + А©у;
б) Х=, дву/дХ^аАвз-То. О*53)
Определив выражение для ©, из решения уравнения (1.52) с граничными условиями (1.53), решение для ©2 можно найти
с помощью преобразования равенства (1.49) к виду
02 = е’+7Ж + 0Г«‘ {1’54)
Анализ полученного в работе [40] точного решения уравнений ‘(1-49) и (1.50) позволил обосновать следующие пригодные для практических расчетов приближенные выражения для 0( и 02:
01 = — Tja + [(©„ + Tja) (1-о) + Д©ус] X, + (а Д03 — Т0) Y{, (1.55) 02 = [(©„ + Tja) (1 — а) + Д©уо] Х2 + (а Д03 — Т0) У2, (1.56)
где
TOC o "1-5" h z v S2e-s2-<i-X)S, _sles>x л,— д — ;
(о + oS2/Я — 1) e-s‘ (1~Х) — (0 + aSi/a — 1) es*x~s>. rl— D
V S2(l+Ss/a)es’ —(o + oS,/a)eS2*-Sl
Л2_ _ ,
v (o + oS2/a-l)e-s’il~x)-(c-oSi/a-l) (l+S2/a)es*x~s’ . r2 _ _ ,
D — S] (o + aS2/a — 1) — S2 (a 4- aSJa — 1) eS2~Sl.
При a = 0 схема циркуляции разомкнутая, при er = 1 система циркуляции замкнутая.
В последних выражениях Si и S2 — корни характеристического уравнения:
S], 2 == + *Jb kxj4 4" abkx.
При расчетах с помощью полученных аналитических выражений для ©1 и 02 необходимо определить среднее по глубине скважины значение коэффициента нестационарного теплообмена в соответствии со следующим равенством:
К (Fo) = kx (Fo) ~k* (F°)> ‘ (1 -5-7)
где H = H0 4- vMFoRo/an — глубина скважины на момент расчета
~ 1 Г
ее температурного режима; k% (Fo) = — р^- kxd Fo — среднее интегральное по времени значение.
Из выражения (1.57) видно, что если бурение скважины ведется непрерывно с нулевой глубины (Но — 0) или глубина скважины, с которой начался цикл бурения, значительно меньше глубины скважины, для которой выполняется расчет (Яо ^ Я), то следует принимать kx(Fo) = kx{Fo). В случае, когда температурный режим скважины рассчитывается для интервала времени, в течение которого ее глубина по сравнению с первоначальной существенно не меняется (Я « Но), то тогда fcT(Fo) = fex(Fo).
В работе [23] предложены следующие приближенные зависимости для определения kx и kx, точность которых удовлетворяет
в большинстве случаев требованиям технологических и технических расчетов:
——- 2^—; (1.58)
1 + ВІ
Ь = —————- “————— ; (1 .59)
х 1 + Ві 1п (1 4-2 -/Ро) ‘
|
Здесь |
 кх=±кг. (1.60)
кх=±кг. (1.60)
ВІ = «с^оАп-
Для расчета температурного режима бурящейся скважины рекомендуются следующие зависимости для определения основных •теплофизических параметров, входящих в расчетные формулы
[5, 23].
Для буровых растворов
а£ = (Я/4) Ыиь і=1, 2с, где число Нуссельта или безразмерный коэффициент теплоотдачи ( 0,15 Ие0-33 Рг0>,Юг, Ие < Кекр;
N11;
,023 Ре°-8Рг°14, Ие > Рекр.
Здесь Ие == сх^эр/цг — критерий Рейнольдса, определяющий характер течения среды; Рг = ц/(яр)—критерий Прандтля, характеризующий соотношение между кинематическими и тепловыми свойствами среды; Ог = Р(£р2/2/м.2)А/— критерий Грасгофа, характеризующий процесс естественной конвекции в жидкости; I — характерный размер; Р=(р — ро)/р — температурный коэффициент объемного расширения, р0 и р — плотность холодной и нагретой жидкости, Д^ — температурный перепад в жидкости.
В зависимости от реологических свойств бурового раствора при расчете безразмерных критериев Ие, Рг и (лг используются значения динамической ц, структурной г) и эффективной г)Эф вязкости.
Значение Иекр, определяющего момент перехода ламинарного режима в турбулентный (и обратно), также зависит от реологических свойств растворов. Для ньютоновских жидкостей ИеКр = = 2320. Данные по различным неньютоновским буровым растворам приведены в работах [1, 5].
Для бурения скважин с продувкой воздухом критерий N11 определяется выражением
Ыиг = 0,018 Кег’8, /=1,2, с.
Во всех расчетных формулах йэ = 2г1 при 1 = 1 и с1э — 2(/?0 —
— г2) при 1 — 2, с.
Местный прирост температуры промывочной среды у забоя
|
Таблица 1.8 Исходные данные для расчета температурного режима бурящихся скважин
|
|
Расчетные параметры н критерии |
|
Параметры и критерии |
Варианты |
|||
|
1 |
2 |
3 |
4 |
|
|
vu м/с |
0,204 |
0,212 |
0,868 |
13,26 |
|
о2, м/с |
0,839 |
0,872 |
0,424 |
15,55 |
|
11 178 |
9 739 |
1 089 |
107 574 |
|
|
Яе2 |
4 597 |
4 006 |
260 |
34 158 |
|
Рг |
5,85 |
9,53 |
21,04 |
0,722 |
|
<Хі, Вт/(м2-°С) |
609 |
823 |
212 |
1 17 |
|
а2, Вт/(м2 • °С) |
2 910 |
4 005 |
725 |
71,8 |
|
Ко, Вт/(м2 • °С) |
478 |
637 |
161 |
44,2 |
|
а |
127,7 |
95,5 |
0,994 |
18, 35 |
|
Ь |
0,339 |
0,190 |
0,0117 |
0,789 |
|
ВІ |
79,0 |
153,7 |
14,8 |
1, 47 |
|
Бо |
3/6 |
3/6 |
2/4 |
2/4 |
|
кх, Вт/(м2 • °С) |
24,4/20,6 |
17,5/14,8 |
34,1/29,2 |
24,1/21,3 |
|
ві |
36,9/33,6 |
19,6/17,8 |
0,86/0,78 |
30,5/28,0 |
|
$2 |
—28,6/—26,6 |
— 16,2/—15 |
—0,46/—0,44 |
—11,5/—11,С |
|
Таблица 1.9 |
|
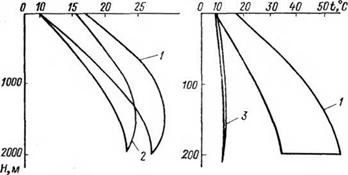
а 6
Рис. 1.13. Распределение температуры промывочной среды в бурящейся скважине. о. •— варианты 1 и 2; б — варианты 3 и 4. |
В качестве примера использования полученных приближенных решений проведем расчеты по следующим четырем вариантам (рис. 1.13).
Вариант I. Глубокое разведочное бурение, промывочная среда — полимерный раствор.
Вариант 2. Глубокое разведочное бурение, промывочная среда— техническая вода.
Вариант 3. Бурение неглубоких скважин, промывочная среда — глинистый раствор.
Вариант 4. Бурение неглубоких скважин, промывочная среда — сжатый воздух.
Значения исходных данных для расчетов приведены в табл. 1.8, а значения параметров и критериев даются в табл. 1.9.
Необходимые для тепловых расчетов значения физических и теплофизических характеристик горных пород и буровых промывочных агентов приведены в прил. 1 и 2.
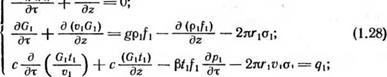
![ПРИБЛИЖЕННЫЕ МЕТОДЫ РЕШЕНИЯ ЗАДАЧ О ТЕМПЕРАТУРНОМ РЕЖИМЕ СКВАЖИН ПРИ БУРЕНИИ Подпись: :[2^1(02_@1)_ 2я^ас.(02_0п)]я + £Н_ (1.40) (1.41)](/img/814/image061.gif)