BURST PRESSURE
BURST PRESSURE
Burst pressure originates from the column of drilling fluid and acts on the inside wall of the pipe. Casing is also subjected to kick-imposed burst pressure if a kick occurs during drilling operations.
|
|
|
/ / / |
—p. j — |
/ / И |
|
|
■* a, *■ |
(b)
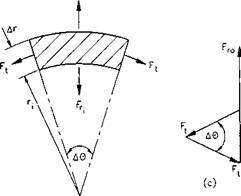
Fig. 2.6: Free body diagram of the pipe body under internal pressure.
The free-body diagram for burst pressure acting on a cylinder is presented in Fig. 2.6. If a ring element subtends an angle A9 at any radius r while under a constant axial load, then the radial and tangential forces on the ring element are given by:
radial force: FT = p, Ax г, Ав
tangential force: 2Ft = 2 at Ax A r,
where:
a( = tangential stress due to internal pressure, psi.
Pi = internal pressure, psi.
r, = internal radius of casing, in.
From the equilibrium condition of the small element one obtains:
|
(2.53) |
Pi Ax rt Ав = 2a t sin — Ax A r
For small Ав, sin(A0/2) и Ав/2, an(i Eq. 2.53 reduces to: Д r
Pi — <?t —
For a thin-walled cylinder with a high nominal diameter to thickness ratio and <T( equal to <ry, the yield strength of the pipe material. Eq. 2.54 can be expressed as follows:
|
(2.55) |
p‘= 2<7′ Ш
where:
d0 — outside diameter of the cylinder, in.
t — cylinder wall thickness, in.
рь — burst pressure rating of the material, psi.
|
|
Equation 2.55 is identical to Barlow’s formula for thick-walled pipe which is derived using the membrane theory for symmetrical containers. If the wall thickness is assumed to be very small compared to the other dimensions of the pipe the axial stress can be considered to be zero. In this case the tangential and radial forces are the principal forces along the principal planes.
|
|
|
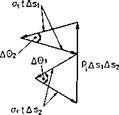
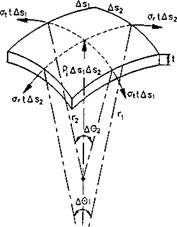
Fig. 2.7 : Free body diagram of a rectangular shell element under internal pressure. |
A small element (Д-Si хД«2) of a container, which is subjected to a burst pressure of is included between the radii rq and r2. A9i and Д92 denote the angles be
tween the radii rq and r2, respectively. Figure 2.7 presents the free-body diagram of the element used to derive Barlow’s formula. From the equilibrium conditions of the element one obtains (assuming sin(A0/2) ~ A9/2:
Д0, A9>
— 2 art As-2 ——— 2at t Asi ——f — p, A. S] As2 — 0 (2.56)
If Asi — riAOi, and As2 = r2A92. then Eq. 2.56 becomes:
^ + ^ = ^1 (2.57)
r i r2 t
If a cylindrical pipe of radius r is subjected to an uniform internal pressure p, and ?q tends to infinity, then the equation of thick-walled pipe is:
Expressing the equation in terms of nominal diameter, d0. and yield strength of the pipe body, cry, one obtains Barlow’s formula:
= ТГШ {2M)
The API burst pressure rating is based on Barlow’s formula. The factor of 0.875 assumes a minimal wall thickness and arises from the 12.5 % manufacturer’s tolerance allowed by the API in the nominal wall thickness. Thus, the burst pressure rating is given by:
pbr = 0-875-^- (2.60)
where:
Pbr = burst pressure rating as defined by the API.
Calculate the burst pressure rating of X-80, 47 lb/ft. 9| in. casing.
From Eq. 2.60:
‘0.472 V
Pbr = 0.875 x ^2 x 80,000 x (g ^г)) =
This figure represents the minimal internal pressure at which permanent deformation could occur provided that the pipe is not subjected to external pressure or axial loading.