Бурение грунтовых зондов, установка энергетических колодцев

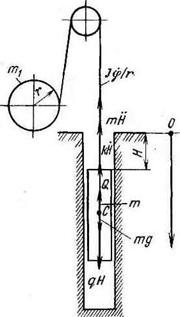
Усложним рассмотренную выше задачу. На рис. 7.4 представлена схема действия сил на падающий инструмент при ударно-канатном бурении «клюющим» способом. Введем следующие допущения: 1) ин­струмент падает с уровня земли; 2) приращение силы тяжести инструмента за счет сматывания каната прямо пропорционально глубине скважины Н; 3) приращение ускорения лебедки за счет уменьшения диаметра барабана при сматывании каната отсутствует; 4) на инструмент действуют постоянные сопротивления и сопротив­ления, пропорциональные скорости (такое допущение справедливо для случая движения инструмента в скважине, не заполненной водой).

Рис. 7.4. Схема действия сил иа пада — .ющий в скважину инструмент

С учетом принятых допущений на основании принципа Даламбера для представленной на рис. 7.4 системы может быть записано следующее дифференциальное уравнение движения инструмента:

mH+J — +к Н—q Н=mg—Q,

Г

где т — масса инструмента; Н—ускорение движения инструмента; J—момент инерции лебедки относительно оси вращения; ср—угол поворота барабана лебедки: ср — угловое ускорение вращения барабана лебедки; /• — радиус барабана лебедки; к — коэффициент сопротивления движению инструмента; Н—скорость движения инструмента; q— вес 1 м каната; Q—постоянные сопротивления (сопротивления сухого трения).

Для упрощения примем, что J=mlr2/2, где т—масса лебедки. Будем учитывать, что ф — Я/r. Тогда уравнение (7.18) можно записать в виде

(m + ml/2)H+kH-qH=P-Q,

где Р=mg — вес инструмента.

Следует иметь в виду, что коэффициент сопротивлений, пропор­циональных скорости, включает две составляющие; к j —сопротивления во вращающихся частях лебедки и блока; к2—сопротивления при 11 3477 161

движении инструмента в скважине (k—ki+ki). Точно так же посто­янные сопротивления Q могут быть разложены на две составляющие: Qi—сопротивления сухого трения во вращающихся частях; 62— сопротивления сухого трения в скважине (6 = 61+62)- Поскольку каждая из названных характеристик к, ■> и 61,2 обладает аддитивным свойством, в последующих вычислениях мы будем использовать комплексные характеристики к и Q.

С учетом начальных условий Н=О, Н=0 при г=0 решение уравнения (7.19) имеет вид

TOC o "1-5" h z „-‘-еГ *(<*•+»*■) .1 (72С)

Ч [.2 2Jk2+4(m+0,5mAq J

где р и р’2—корни характеристического уравнения дифференциаль­ного уравнения (7.19),

-к± Jk2+4(m + 0,S"h)4 Рхг 2(/и+0.5ш,) ’ ( )

Скорость движения инструмента по скважине определяется вы­ражением

у=-1______ ? ~ , (е^.’+е^1). (7.22)

y/ki+4(m+ii,5mi)q

Детальную проверку закона движения инструмента по скважине провел Б. В. Цынский. Дадим краткий анализ полученных результатов.

На скорость движения снаряда в момент удара о забой опре­деляющее влияние оказывает вес инструмента (точнее, разность между весом инструмента Р и постоянными сопротивлениями Q); очевидно, что при их равенстве и <7=0 движение инструмента вообще проис­ходить не будет. При большом весе инструмента (более 5 кН) влияние сопротивлений, пропорциональных скорости, на скорость движения инструмента в момент удара незначительно, однако оно существенно возрастает при малом весе инструмента (менее 1 кН). Предельная скорость инструмента в этом случае при к=200 Н — с • м-1 составляет примерно 5 м-с’1. Такую скорость инструмент приобрета­ет уже при высоте сбрасывания 5 м. Дальнейшее увеличение высоты сбрасывания к повышению скорости движения инструмента в момент удара о забой не приведет.

На скорость движения инструмента определенное влияние оказы­вает масса вращающихся частей лебедки и блоков и вес сматыва­ющегося с лебедки каната. Масса вращающихся частей снижает эту скорость, а вес каната — увеличивает. При используемых в настоящее время канатах влиянием q можно пренебречь.

Оптимальная высота сбрасывания инструмента при бурении сква­жин большого диаметра (более 0,5 м) составляет 6—7 м, при бурении скважин диаметром менее 0,2 м—8—10 м. Дальнейшее увеличение 162

Комментарии запрещены.