Бурение грунтовых зондов, установка энергетических колодцев

В разделе 3.3 давалось определение абсолютно твердого тела. Расстояние между любыми двумя точками этого тела всегда остается постоянным. Иными словами, ни одна точка твердого тела не может удалиться от другой или приблизиться к ней даже на ничтожно малое расстояние. Это играет очень большую роль в кинематике твердого тела. Естественно, подобных твердых тел в природе не встречается, любое тело под действием нагрузок изменяет свою 102

‘ форму и геометрические размеры. Однако в кинематике при рас­смотрении движения тел эти изменения размеров тел по сравнению С проходимыми точками расстояниями столь малы, что ими вполне можно пренебречь.

Задачи кинематики твердого тела состоят в следующем: 1) задание движения и определение кинематических характеристик всего зела в целом; 2) определение кинематических характеристик каждой точки тела.

Различают следующие виды движения твердого тела: поступатель­ное, вращательное, плоско-параллельное, вокруг неподвижного центра и общна случай движения свободного твердого тела в пространстве. ‘Ниже будут кратко рассмотрены поступательное, вращательное и пло­ско-параллельное движения твердого тела, как наиболее часто ре­ализуемые в бурении.

Поступательным называется такое движение твердого тела, при котором любая прямая линия, проведенная в этом теле, перемещается, оставаясь всегда параллельной себе.

При поступательном движении тела траектории его точек могут быть любыми кривыми линиями, в том числе окружностями. Применительно к твердому телу, нельзя, например, сказать, что оно движется прямолинейно. Во всяком случае, здесь скрыта определенная неточность. Более правильно сказать, что тело движется поступатель­но, а его точки — прямолинейно. —

При поступательном движении точки твердого тела перемешаются по одинаковым, при наложении совпадающим, траекториям, с оди­наковыми по модулю и направлению скоростями и ускорениями. Следовательно, поступательное движение вполне определяется движе­нием любой его точки. Общая для всех точек тела скорость v называется скоростью поступательного движения тела, а ускорение w—ускорением поступательного движения. Во всех остальных случаях точки тела движутся с разными скоростями и ускорениями.

Задача изучения кинематических характеристик поступательно движущегося твердого тела, таким образом, сводится к изучению кинематики точки, для чего применим математический аппарат, приведенный в двух предыдущих разделах.

В качестве поступательно движущихся элементов из области бурения могут быть названы следуюнще виды движений: бурового снаряда в скважине с прямолинейной осью без раскачивания и враще­ния. траверсы или шпинделя станка, корпуса станка вдоль рамы при его отодвигании от устья скважины, поршня или плунжера в насосе, корпуса вибропогружателя в направляющих мачты и т. д. Во всех перечисленных случаях точки перемещающихся тел движутся прямолинейно. Устройства с поступательно движущимися элементами, точки которых совершали бы криволинейное движение, в разведочном бурении используют сравнительно редко.

Вращательным называется такое движение твердого тела, при котором какие-нибудь две точки (например, А и В), принадлежащие телу (или неизменно с ним связанные), остаются в течение всего времени движения неподвижными.

Проходящая через неподвижные точки А и В прямая называется осью вращения. При вращательном движении точки, принадлежащие оси вращения, будут неподвижны, а остальные точки тела будут описывать окружности, плоскости которых перпендикулярны к оси окружности, а центры лежат на этой оси.

Положение вращательно движущегося тела определяется углом <р поворота этого тела, который отсчитывают от некоторой неподвижной плоскости, проведенной через ось вращения. Обозначим эту ось буквой z. Будем считать угол ф положительным, если он отложен от неподвижной плоскости в направлении против хода часовой стрелки (для наблюдателя, смотрящего с положительного направления оси z), и ртрицательным, если по ходу часовой стрелки. Чтобы знать положение тела в любой момент времени, надо знать зависимость угла <р от ( времени:

<Р =/(*)- (5.20)

Приведенное уравнение выражает закон вращательного движения твердого тела. Угол поворота ф измеряется в радианах (по существу, является безразмерной величиной).

Основные кинематические характеристики вращательного движения твердого тела—его угловая скорость со и угловое ускорение в.

Угловая скорость тела определяется выражением

со=dq>/dt. (5.21)

Знак при букве со определяет направление вращения тела. Когда вращение происходит против хода часовой стрелки, то со>0 и имеет знак плюс, а когда по ходу, то со<0, т. е. имеет знак минус. Размерность угловой скорости

Угловую скорость со принято изображать в виде вектора со, который направлен вдоль оси вращения в ту сторону, откуда вращение видно происходящим против хода часовой стрелки. Следует иметь в виду, что вектор угловой скорости всегда направлен перпендикулярно к плоскости вращения тела. Для определения направления вектора угловой скорости пользуются правилом правого винта.

Угловое ускорение характеризует изменение угловой скорости с течением времени

E—dio/dt~d2q>ldt2. (5.22)

Размерность углового ускорения в с“2.

Если модуль угловой скорости со временем возрастает, вращение тела называется ускоренным, а если убывает—замедленным. Легко видеть, что вращение будет ускоренным, когда величины со и в имеют одинаковые знаки, и замедленным, когда разные.

Угловое ускорение тела (по аналогии с со) можно также изобразить в виде вектора ё, направленного вдоль оси вращения также по правилу правого винта.

.Рис. 5.4. К определению ускорения Рис. 5.5. К определению уравнений точки вращающегося твердого тела плоскопараллельного движения

(5.23)

Если <о=const, вращение тела называют ‘равномерным. Закон равномерного вращения имеет вид

Ф = ф0+со0<,

где ф0 и со0—начальные угол поворота тела и угловая скорость.

Если e=const, вращение тела называют равнопеременным. Закон равнопеременного вращения записывается в виде

(5.24)

Ф = фо/ — ре г2/2.

Линейная скорость любой точки вращающегося твердого тела, отстоящей от оси вращения на расстоянии А будет

(5.25)

г = Асо.

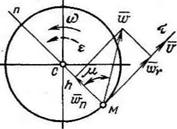
Скорость v точки М направлена по касательной к окружности, которую описывает точка М.

Линейное ускорение любой точки вращающегося твердого тела определяется через его касательную со. и нормальную и>„:

гс, = Ае, *v„ = Лсо2.

(5.26) (5.27)

Касательное ускорение всегда направлено по касательной к тра­ектории (в сторону движения, если тело вращается ускоренно, или в обратную сторону, если тело вращается замедленно); нормальное ускорение wn всегда направлено вдоль радиуса А к оси вращения (рис. 5.4).

Полное ускорение точки

(5.28)

w=A(e2+co4)1^.

Отклонение полного ускорения от радиуса описываемой точкой окружности определяется углом р, который вычисляют по формуле

Вращательное движение совершают многочисленные элементы различных машин, применяемых в разведочном бурении (шестерни, шкивы, шпиндели, вращатели, кривошипы и другие детали буровых станков и установок, двигателей, насосов, транспортных средств, вспомогательных приспособлений и устройств и т. д.). Без преувеличе­ния можно сказать, что вращательное движение является основным видом движения твердых тел, используемым в разведочном бурении.

Наконец, плоскопараллельным (или плоским) называется такое движение твердого тела, при котором все его точки перемещаются параллельно некоторой неподвижной плоскости. Поэтому для изучения движения тела ограничиваются изучением движения какого-либо сечения тела, параллельного этой неподвижной плоскости.

Положение сечения тела (S) в плоскости Оху определяется положением какого-нибудь проведенного в этом сечении отрезка АВ (рис. 5.5). В свою очередь, положение отрезка АВ можно определить, зная координаты хА и уЛ точки А и угол ср, который отрезок АВ образует с осью х. Точку А, выбранную для определения положения сечения называют полюсом. Очевидно, что при движении тела величины хЛ и ул и ср будут изменяться. Чтобы знать закон движения тела, т. е. его положение в пространстве в любой момент времени, надо знать зависимости

(5.30)

xA=fi(t), }’А —/г (О — Ф=/з(0-

Приведенные уравнения называют уравнениями плоскопараллельного движения твердого тела.

Плоскопараллельное движение твердого тела можно рассматривать как сумму поступательного движения, при котором все точки тела движутся так же, как полюс А, и вращательного движения вокруг этого полюса. Поступательная часть описывается первыми двумя уравнениями (5.30), а вращательная — третьим. В качестве полюса может выбираться любая точка сечения тела.

Основные кинематические характеристики плоскопараллельного движения — скорость и ускорение поступательного движения, равные скорости и ускорению полюса vA и wA, а также угловые скорость (о и ускорение е вращательного движения вокруг этого полюса. Значение этих характеристик можно найти из приведенных выше трех уравнений плоскопараллельного движения.

Скорость любой точки В тела складывается геометрически из скоростей, которые она получает в каждом из указанных выше движений:

vB=vA+vBA, (5.31)

(5.32)

где vB—скорость любой точки сечения тела; vA—скорость полюса; vBA—скорость точки В в ее движении по окружности вокруг полюса,

vba=(oBA,

о—угловая скорость тела; АВ—расстояние от полюса до данной точки В.

Скорость vBa всегда перпендикулярна к отрезку В А. Определение скоростей точек с помощью приведенного выше [векторного равенства (5.31) связано с некоторыми неудобствами. — Исходя из прлученного результата можно установить друтие более [простые методы определения скоростей точек тела. Один из этих [методов основан на следующей теореме — проекции скоростей двух В, точек твердого тела на прямую, соединяющую эти точки, равны [друг другу:

(5.33)

vA cosa=rBcos р,

[‘ Где а и р — углы, составленные векторами скоростей точек А и В с пря­мой АВ.

С помощью выражения (5.33) легко находить скорость данной точки тела, если известны направление движения этой точки и скорость какой-нибудь другой точки того же тела.

Второй метод основан на понятии «мгновенный центр скоростей». . Мгновенным центром скоростей называется точка р сечения тела, скорость которой в данный момент времени равна нулю. Мгновенный центр скоростей может располагаться и вне сечения тела, но в этой же плоскости. Легко убедиться, что если тело движется непоступа­тельно, то. такая точка в каждый момент времени существует и притом она единственная.

(5.34)

Мгновенный центр скоростей располагается в точке пересечения I; — перпендикуляров к скоростям точек сечения тела, восстановленных в этих точках. Скорость любой точки тела, лежащей в сечении (5), равна ее линейной скорости при движении по окружности вокруг мгновенного центра скоростей:

v„ = oMp.

Из последнего равенства следует, что скорости точек тела (например, А и В) пропорциональны их расстояниям до мгновенного центра скоростей:

vAlpA = vB/pB. (5.35)

(5.36)

Угловая скорость тела в каждый данный момент времени равна отношению скорости какой-нибудь точки сечения к ее расстоянию от мгновенного центра скоростей р:

со=vB/pB.

Угловая скорость тела может быть также определена, если известны модули и направления скоростей двух точек тела и рас­стояние между этими точками по формуле:

SHAPE * MERGEFORMAT

(5.37)

о>=-

I йв I ВА

(5.38)

(5-39)

(5.40) (5.41)

К частным случаям определения мгновенного центра скорое гей* относятся следующие. а 1. Если плоскопараллельное движение осуществляется путем! качения без скольжения одного цилиндрического или нецилиндричес-^ кого тела по поверхности другого, причем второе тело неподвижно,;! то точка касания р имеет в данный момент времени скорость,]! равную нулю, и, следовательно, является мгновенным центром] скорости. 1 2. Если скорости точек А я В сечения тела параллельны дру™ другу и направлены в одну сторону, причем линия Л В не перпен-3 дикулярна к одной из скоростей, то мгновенный центр скоростей! лежит в бесконечности, и скорости всех остальных точек параллельны] и равны между собой. Этот случай носит название мгновенно! поступательного распределения скоростей. Угловая скорость тела]| в этот момент времени равна нулю. I 3. Если скорости точек А я В тела параллельны друг другу и при; этом линия А В перпендикулярна к одной из скоростей, то мгновенный i центр скоростей р определяется геометрическим построением либр: составлением пропорции (5.35). В этом случае для нахождения точки р надо, кроме направления, знать модули скоростей точек А и В. J 4. Если известны вектор скорости vB какой-нибудй точки сечения! (S) и угловая скорость со поворота тела, то положение мгновенного!! центра скоростей р, лежащего на перпендикуляре к vB, можно найти! из равенства (5.36). 3 Таким образом, плоскопараллельное движение слагается из по-| следовательных мгновенных элементарных поворотов вокруг непре — i рывно меняющих положение мгновенных центров (осей) вращения. 1 Рассмотрим определение ускорений точек тел при плоскопарал-^ лельном движении. Ускорение, например, точки М сечения тела, ( геометрически складывается из ускорения какой-либо другой точю j А, принятой за полюс, и ускорения точки М в ее вращении вместе} с телом вокруг этого полюса 1

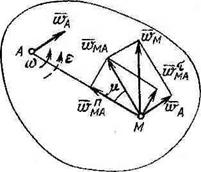
Причем ускорение wMA в движении точки по окружности вокруг полюса

При решении, задач удобно вектор wMA заменять его касательной wxMA я нормальной w"MA составляющими:

Вектор н’ма направлен перпендикулярно к МА в сторону направ­ления углового ускорения тела; вектор irjfx всегда направлен от точки М к полюсу А.

w’MA = МАг Wma = МАч>2.

«Эм(еа+юТг.

Й’м = Я ‘А + Я ‘м А.

Рис. 5.6. К определению ускорения ‘ точки М тела при плоскопараллель — 1 ном движении

I

Тогда (рис. 5.6)

. ’ (5-42)

Если полюс движется непрямолинейно, то его ускорение также. будет слагаться из касательного и нормального, и формула (5.42) примет вид

Wm = wxa+wa +wma + wma — (5-43)

Аналитически wM определяется методом проекций на произвольно ‘ выбранные оси координат. ‘ i

Плоскопараллельное движение в буровых установках совершают : подвижные блоки полиспастов, шатуны двигателей и насосов, сател — литные шестерни планетарных лебедок, колеса транспортных средств на участках дорог при отсутствии поворотов и др.

Комментарии запрещены.