Основные формулы алгебры Формулы сокращенного умножения

16.10.2013 | Автор: admin

(а + Ь)(а — Ь) = а2 + Ь2 (а + Ь)2 = а2 + 2ab + Ь2 (а-Ь)2 = а2 — 2ab + Ь2 (а + b)3 = а3 + 3а2Ь + Зя/>2 + Ь3 (а — 6)3 = а3 — Зя26 + Зяб2 — Ь3

(а + b)(a2 — ab + Ь2) = а3 + Ь3 (а — b)(a2 + ab + Ь2) = а3 — Ь3.

Действия со степенями и корнями

am-bm =(ab)m; Іа-ІЬ=ІаЬ

ат ап = ат*п Іа" =(rfa)" ат :ап — ат~п ф/а =

Дробные и отрицательные показатели

т = [а ат = [а"

а~т = —; ат ат

Основные формулы алгебры Формулы сокращенного умножения

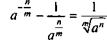
Система уравнений первой степени с двумя неизвестными

Основные формулы алгебры Формулы сокращенного умножения

Неполные квадратные уравнения

ах2 = 0, xt 2 = 0;

ах2 + Ьх = 0, Х = 0, х2 = — —.

2.1 /л — b±yjb2 — Лас

Подпись: 2.1 /л -b±yjb2 - Лас Полные квадратные уравнения

2а

Подпись: 2а ах2 +Ьх + с = О, ДГ| 2 =

— Q-

Подпись: - Q-

V2,

Подпись: V2, x2 + px + q = О, *К2 =-у +

Логарифмы

Если у = Ь то х = Ig^ (b — основание логариф^О, IgO = -°°, Igl = = 0, lg^ = 1; %(тт) = lg/w + lgп; *8“ = lg/w-lg/t; lg/w" = п%т

lg yfni = — lg/w. n

Если b — 10, то логарифм называется десятичным (обыкновенным, бригговым) и обозначается «lg», т. е. без индекса, указывающего на основание логарифма. Далее приведена табл. 1.1.

1.1.1. Основные формулы тригонометрии Функции одного угла

• 2 2 . S>ntt. • I

sin2 а + cos2 а = I; — = tga; sin a cosec а = I;

cos а

cos a

tg2 a + l = sec2 a; —- = ctga; cosaseca = I;

sin a

ctg2 a + I = cosec a; tgactga = l.

Функции дополнительного угла sin(90° — a) = cos a; tg(90° — a) = ctg a; sec(90° — a) = cosec a. Функции суммы и разности двух углов

sin(a±p) = sinacos(3±sinpcosa; cos(a±(3) = cos a cos р ± sin р sin a;

tg(„±p)=Js^±isJL.

I ± tg a tg p

Таблица для вычисления степеней, корней и других величин

Число — диаметр

Кубический

корень

1,0000

1,2599

1,4422

1,5874

1,7100

1,8171

1,9129

2,0000

2,0801

2,1544

2,2240

2,2894

2,3513

2,4101.

2,4662

Квадратный

корень

1,0000

1,4142

1,7321

2,0000

2,2361

2,4495

2,6458

2,8284

3,0000

3,1623

3,3166

3,4641

3,6056

3,7417

3,8730

Киадрат

Куб

Логарифм

Длина

окружности

3,142

6,283

9,425

12,566

15,708

18,850

21,991

25,133

28,274

31,416

34,558

37,699

40,841

43,982

47,124

Площадь

круга

0,7854

3,1416

7,0686

12,5664

19,6350

28,2743

38,4845

50,2655

63,6173

78,5398

95,0332

113,0970

132,7320

153,9380

176,7150

0,00000

9,30103

0,47712

0,60206

0,69897

0,77815

0,84510

0,90309

0,95424

1,00000

1,04139

1,07918

1,11394

1,14613

1,17609

27 64 125 216 343 512 729 1 ООО 1 331

1 728

2 197

2 744

3 375

100

121

144

169

196

225

4 096 4913

5 832

6 859 8000 9261 10648

12 167

13 824

16 625

17 576 19 683 21952 24 389 27 000 29 791

32 768

Число — диаметр

Квадратный

корень

4.0 4,1231 4,2426 4,3589 4,4721 4,5826 4,6904 4,7958 4,8990

5.0 5,0990 5,1962 5,2915 5,3852 5,4772 5,5678

Кубический

корень

2,5198

2,5713

2,6207

2,6684

2,7144

2,7589

2,8020

2,8439

2,8847

2,9240

2,9725

3,0000

3,0366

3,0723

3,1072

3,1414

Куб

Логарифм

Квадрат

Длина

окружности

50,265

53,407

56,549

59,690

62,832

65,973

69,115

72,257

75,398

78,540

81,681

84,823

87,965

91,106

94,248

97,389

Площадь

круга

201,0620

226,9800

254,4690

283,5290

314,1590

346,3610

380,1330

415,4770

452,3890

430,8740

530,9290

572,5550

615,7520

660,5200

706,8580

754,7680

1,20412 1,23045 1,25527 1,27875 1,30103 1,32222 1,34243 1,36173 1,38021 1,39794 1,41497

»____

1,43136 1,44716 1,46240 1,47712 1,49136

256

289

324

361

400

441

484

629

676

625

676

729

784

841

900

961

024

5,6569

3,1748

,50515

100,531

804,2480

I 089

35 937

5,7446

3,2075

1,51851

103,673

855,2990

1 156

3 934

5,8310

3,2396

1,53148

106,814

907,9200

1 225

42 875

5,9161

3,2711

1,54407

109,956

962,1130

1 296

46 656

6,0000

3,3019

1,55630

113,097

I 017,8800

1 369

50653

6,0828

3,3322

1,56820

116,239

1 075,2100

1 444

54 872

6,1644

3,3620

1,57978

119,381

134,1100

1 521

59319

6,2450

3,3912

1,59106

122,522

1 194,5900

1 600

64 000

6,3246

3,4200

1,60206

125,660

1 256,6400

1 681

68921

6,4031

3,4482

,61278

128,810

1 320,2500

1 764

74 088

6,4807

3,4760

1,62325

131,950

386,4400

1 849

79 507

6,5574

3,5034

1,63347

135,090

1 452,2000

1 936

85 184

6,6332

3,5303

1,64345

138,230

520,5300

2 025

91 125

6,7082

3,5569

1,65321

141,370

1 590,4300

2 116

97 336

6,7823

3,5830

1,66276

144,510

661,9000

2 209

103 823

6,8557

3,6088

1,67210

147,650

1 734,9400

2 304

10592

6,9282

3,6342

1,68124

150,800

809,5600

2 401

117649

7,0000

3,6593

1,69020

153,940

1 885,7400

2 500

125 000

7,0711

3,6840

,69897

157,080

1 963,5000

Число — диаметр

Кубический

корень

3,7084

3,7325

3,7563

3,7798

3,8030

3,8259

3,8485

3,8709

3,8930

3,9149

3,9365

3,9579

3,9791

4,0000

4,0207

4,0412

Квадратный

корень

7,1414

7,2111

7,2801

7,3485

7,4162

7,4833

7,5498

7,6158

7,6811

7,7460

7,8102

7,8740

7,9373

8,0000

8,0623

8,1240

Логарифм

Квадрат

Куб

Длина

окружности

160,220

163,360

166.500 169,650 172,790 175,930 179,070 182,210

185.350

188.500 191,640 194,780 197,920 201,060 204,200

207.350

Плошадь

круга

2 042,8200

2 123,7200

2 206,1800

2 290,2200

2 375,8300

2 463,0100

2 551,7600

2 642,0800

2 733,9700

2 827,4300

2 922,4700

3 019,0700 3 117,2500 3 216,9900 3318,3100 3421,1900

1,70757 1,71600 1,72428 1,73239 1,74036 1,74819 1,75587 1,76343 1,77085 1,77815 1,7,8533 1,79239 1,79934 1,80618 1,81291 1,81954

2 601 2 704

2 809 2916

3 025 3 136 3 249 3 364 3481 3 600 3 721 3 844

3 969

4 096 4 225 4 356

132651 140608 148877 157464 166 375 175616 185 193 195 112 205 379 216000 226 981 238 328 250047 262 144 274 625 287496

4 489

300 763

8.1854

4,0615

1,82607

210,490

3 565,2500

8,2462

1,83251

213,630

4 624

314432

4,0817

3 631,6800

4 761

328 509

8,3066

4,1016

1,83885

216,770

3 739,2800

343 000

8,3666

4,1213

1,84510

219,910

3 848,4500

4 900

5041

35791

8,4261

4,1408

1,85126

223,050

3 959,1900

373 248

8,4853

4,1602

1,85733

226,190

5 184

4 071,5000

5 329

389 017

8,5440

4,1793

1,86332

229,340

4 185,3900

5 476

495 224

8,6023

4,1983

1,86923

232,480

4 300,8400

5 625

421 875

8,6603

4,2172

1,87506

235,620

4 417,8600

5 776

438 975

8,7178

4,2358

1,88081

238,760

4 536,4600

5 929

456 533

8,7750

4,2543

1,86649

241,900

4 656,6300

6 084

474 552

8,8318

4,2727

1,89209

245,040

4.778,3600

6241

493 039

8,8882

4,2908

1,89763

248,190

4 901,6700

6 400

512000

8,9443

4,3089

1,90309

251,330

5 026,5500

6 561

531 441

9,0000

4,3267

1,90849

254,470

5 153,0000

6 724

551 368

9,0554

4,3445

1,91381

257,610

5 281,0200

6 889

571 787

9,1104

4,3621

1,91908

260,750

5410,6100

7056

592 704

9,1652

4,3795

1,92428

263,890

5 541,7700

7 225

4,3968

614 125

9,2195

1,92942

267,040

5 674.5000

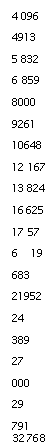Число	Квадрат	Куб	Квадратный корень	Кубический корень	Логарифм	Число — диаметр
Длина окружности	Площадь круга
86	7 396	636 056	9,2736	4,4140	1,93450	270,180	5 808,8000
87	7569	658 503	9,3274	4,4310	1,93952	273,320	5 944,6800
88	7 744	681 472	9,3808	4,4480	1,94448	276,460	6 082,1200
89	7921	704 969	9,4340	4,4847	1,94939	279,600	6221,1400
90	8 100	729 000	9,4868	4,4814	1,95424	282,740	6 361,7300
91	8281	753 571	9,5394	4,4979	1,95904	285,880	6 503,8800
92	8464	778 688	9,5917	4,5144	1,96379	289,030	6 647,6 НЮ
93	8649	804 357	9,6437	4,5307	1,96848	292,170	6 792,9100
94	8836	830584	9,6954	4,5468	1,97313	295,310	6 939,7800
95	9 025	857 375	9,7468	4,5629	1,97772	298,450	7088,2200
96	9216	684 736	9,7980	4,5789	1,98227	301,590	7 238,2300
97	9409	912673	9,8489	4,5947	1,9&677	304,730	7 389,8100
98	9 604	941 192	9,8995	4,6104	1,99123	307,880	7 542,9600
99	9 801	970299	9,9499	4,6261	1,99564	311,020	7697,6900
100	10000	1 000000	10,0000	4,6416	2,00000	314,160	7 853,9800

. Л. . а, /1 — cosa

sin 2 a = 2 sin a cos a; sin —= ±J—- ;

2 V 2_____

Л 2-? ос 11 + cosa cos2a = cos2 a-sin2 a; cos— = ±J ;

1 — tg2 a sin a

Формулы для приведения тригонометрических выражений к виду, удобному для логарифмирования

. 0 ~ . a + В а-В. • о л • а-р а + р

sina + sinp = 2sin—y^-cos—sina-sinp = 2sin—y-cos—

n ~ a+p a-p. _ _ . a+P. a-p

cos a + cos p = 2 cos ——11 cos ——1-; cos a — sin В = -2 sin—- sin.

2 2 K 2 2

Решение треугольников

Если а, Лис — стороны треугольника, а а, р и у — противолежащие этим сторонам углы, то

sin a sin р sin у

Если треугольник прямоугольный (угол у = 90°), то

а = с • sin a; b = с • cos a a = b — tga; b = a • tgp; ab-b• ctgP; b — a • ctga.

Далее приведены таблица значений sin, cos, tg, ctg для важнейших углов и всех четвертей (табл. 1.2) и формулы приведения для sin, cos, tg’H ctg <p < 90° (табл. 1.3).

Таблица 1.2

Таблица значений sin, cos, tg, ctg для важнейших углов и всех четвертей

Триго-

номет-

риче-

ские

функ

ции

0°

30°

45°

60°

90°

180°

270°

360°

0…

90°

90…

180°

180…

270°

270…

360°

sin

у/2

7з

+ 1

-1

—

cos

-1

+ 1

—

Триго-

номет-

рнче-

ские

функ

ции

0°

30°

45°

60°

90°

180°

270°

360°

0…

90°

— 40

ос о о :

180…

270°

270…

360°

ОО

—

ctg

ОО

л/3

yЯ

ОО

—

Таблица 1.3 Формулы приведения для sin, cos, tg и ctg <р < 90°

Значения угла <р	sirup	С05ф	tg<P	clgy
90° ±ф	+С08ф	±SirUp	±^ф	±tg<P
180° ±ф	±5Шф	-СОЯф	±tg<p	±Ctgф
270° ±ф	-СОБф	±sirup	±ctgi?	±tg9

Рубрика: Справочник бурильщика