Бурение грунтовых зондов, установка энергетических колодцев

Закон распространения тепла путем теплопроводности впервые был установлен в 1882 г. Фурье. Согласно этому закону количество передаваемого тепла Q (в ккал) выражается уравнением

Q = —ХГх 1— — >^т, (1.1)

где X— коэффициент теплопроводности в ккалЫ ■ ч • °С; F— пло­щадь в мг б — толщина слоя в. и; tCl и tc, — температуры на поверх­ности стенки соответственно со стороны входа и выхода теплового потока в °С; т — время в ч.

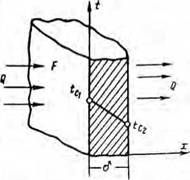
Рас. 2. Распределение темпера­туры при прохождении тепла через плоскую стенку.

Из выражения (1.1) видно, что коэффициент теплопроводности X представляет собой множитель пропорциональности и характери­зует способность вещества проводить тепло. Этот коэффициент выражает то количество тепла в килокалориях, которое проходит в течение 1 ч через стенку толщиной 1 .н и площадью 1 л® при раз­ности температур на поверхностях стенки 1° С (рис. 2).

Каждое вещество имеет опреде­ленный коэффициент теплопроводно­сти, который находится из опытов.

Если от изменения температуры tc, — f0, = Д t на расстоянии б пе­рейти к температурному градиенту по толщине слоя, направленному нормально к поверхности стенки

Iim Тб — = =grad 1 <° С/-и)’

Ai -> О Ц0 ОХ

то выражение (1.1) [можно перепи­сать так:

Q = —XFx ~ = — XFx grad t (ккал).

(I. la)

Здесь знак минус указывает на то, что с увеличением толщины стенки температура убывает.

Очень часто необходимые расчеты ведутся по отношению не ко всему количеству тепла Q, а по отношению к тепловому потоку, отнесенному к единице площади F и единице времени т, т. е. по отно­шению к удельному тепловому потоку q. В этом случае

q — ^Х —(ккал/м2-ч). (1.16)

Как видно из этого выражения, для определения удельного теплового потока необходимо знать коэффициент теплопровод­ности материала, через который передается тепло, а также темпера­турный градиент. Для нахождения этого градиента нужно знать распределение температур, что в общем случае возможно лишь в результате решения дифференциального уравнения теплопровод­ности.

Ч

Известна следующая простая схема вывода этого уравнения, основанная на том, что согласно закону сохранения энергии изме­нение теплосодержания любого элемента объема в теле за любой промежуток времени равно сумме количеств тепла, подведенного

путем теплопроводности и возникшего п результате внутренних источников тепла, т. е.

Л<?1 = А&ТЛ&, (А)

dt

где Д<?1 = СР 57 dV’dt — количество тепла, затраченного на увели­чение теплосодержания тела в объеме dV за время dx AQz — — Xsi^tdVdx — количество тепла, подведенное к объему dV за время dx путем теплопроводности; AQ3 — qv dVdx — количество тепла, возникшее в объеме Д V за время dx. Здесь <?v (в ккал/м3 X г) —произ­водительность внутренних источников тепла.

Подставив эти значения в соотношение (А) и преобразовав его, получим

или

dt _ X (frt I a*t вы n l

dx ср дхг ‘ ду* дг* / ^ rp ^V’ ‘ ‘ ‘

где а — коэффициент температуропроводности, характеризующий

скорость изменения температуры; а — в мг/ч; V2Ј — оператор

Лапласа, представляющий собой символ, при помощи которого обозначают сумму вторых производных (в данном случае темпера­туры) по координатным осям.

Выражение (1.2) является уравнением теплопроводности Фурье в дифференциальной форме. Способы его решения для различных случаев разнообразны.

Если процесс передачи тепла происходит только в одном напра­влении, например в направлении оси х, то уравнение (1.2) упрощается и принимает вид:

di _„&lt | qv /1

dx dxi T tp ‘ ‘

Если при этом процесс установившийся, т. е. ^ = 0, то

-3i* = — T»v <‘-26)

Если внутри объема не выделяется тепло, т. е. qy — 0, то урав­нение (1.2) упрощается:

dt dx

TOC o "1-5" h z 2. {дЧ. , d*t ..

или в цилиндрической системе координат при условии, что тепловое поле обладает осевой симметрией:

at / т, 1 at ач п.. .

• -^=аЫ+Т1>Г+а*)- <L3a>

ю

При наличии установившегося теплового режима, когда Ц — = О,

(1.4)

выражения (1.3) и (1.3а) принимают вид:

^ дуг ‘ дгг и

дхг

a»t, 1 at, т п /т / v

аг* ^ г ar а** * (l-*ia)

Таким образом, если температура исследуемого пространства не изменяется во времени, то уравнение теплопроводности автома­тически переходит в уравнение Лапласа.

Решить уравнение Фурье в условиях неустановившегося режима очень трудно и возможно лить в самых простых случаях.

Комментарии запрещены.